Recent News

Unlocking the Power of Wavevector: The Key to Quantum and Material Insights

Posted on
Unlocking the Power of Wavevector: The Key to Quantum and Material Insights

Wavevector Demystified: How This Fundamental Concept Shapes Quantum Physics, Materials Science, and Beyond. Discover the Hidden Patterns That Govern Waves and Particles.

Introduction to Wavevector: Definition and Historical Context

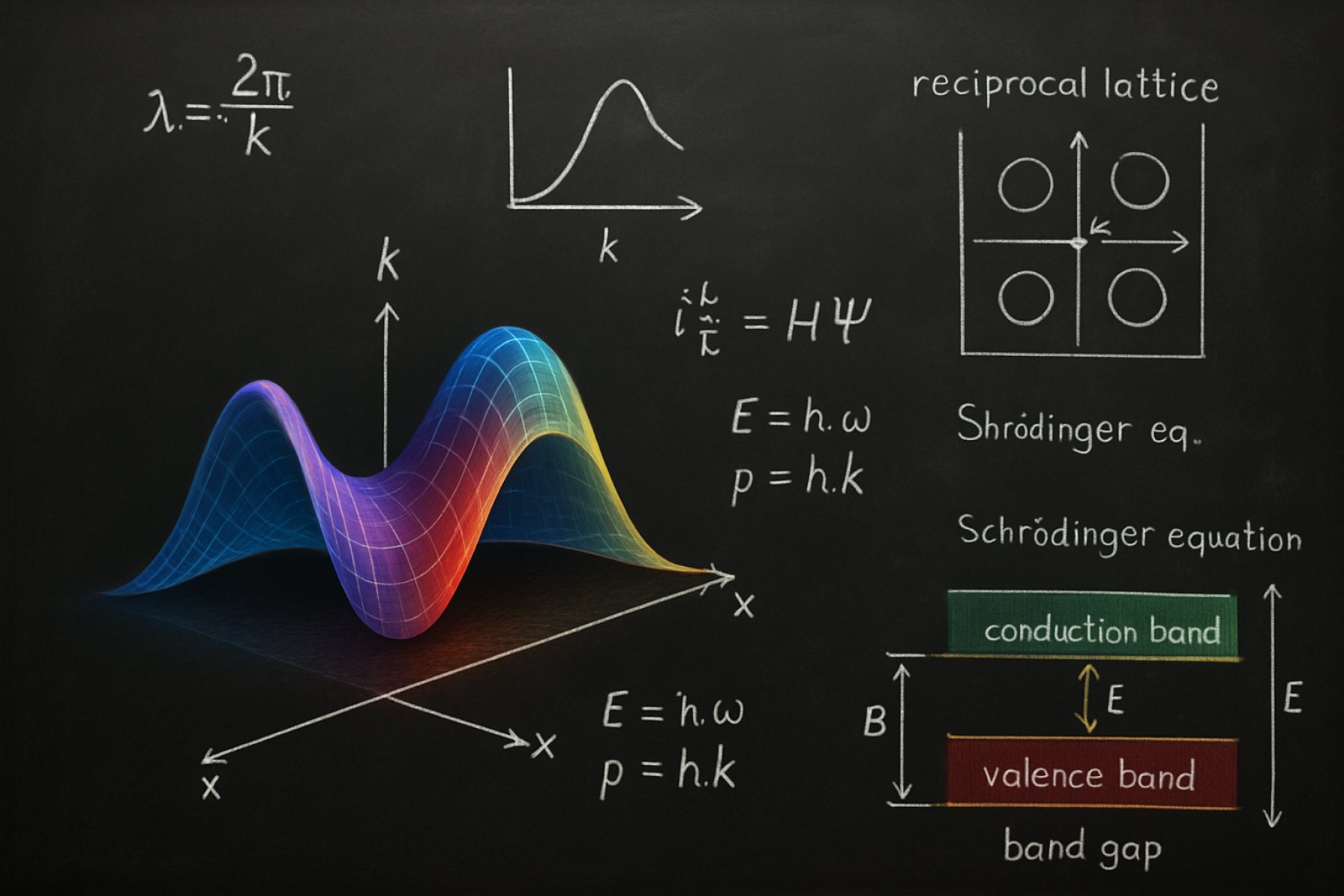
The concept of the wavevector is fundamental in the study of wave phenomena across physics, including optics, acoustics, and quantum mechanics. A wavevector, typically denoted by the symbol k, is a vector quantity that characterizes both the direction of propagation and the spatial frequency of a wave. Mathematically, the magnitude of the wavevector is given by ( |k| = 2pi/lambda ), where ( lambda ) is the wavelength. The direction of the wavevector points in the direction in which the wave propagates. This dual role makes the wavevector a central tool in describing periodic phenomena, such as electromagnetic waves, sound waves, and the quantum mechanical wavefunctions of particles.

Historically, the wavevector concept emerged from the development of wave theory in the 19th century, particularly as scientists sought to mathematically describe light and sound as waves. The formalization of the wavevector was closely tied to the advent of Fourier analysis, which allowed complex waveforms to be decomposed into sums of sinusoidal components, each characterized by a specific wavevector. In the context of crystallography and solid-state physics, the wavevector became especially important for describing the behavior of electrons and phonons in periodic lattices, as seen in the development of band theory and Brillouin zones.

In modern physics, the wavevector is indispensable. In quantum mechanics, for example, the wavevector is directly related to the momentum of a particle via the de Broglie relation ( p = hbar k ), where ( hbar ) is the reduced Planck constant. This relationship underpins much of quantum theory and is foundational in the study of electron behavior in materials. In optics, the wavevector describes the propagation of light in different media, influencing phenomena such as refraction and diffraction. The wavevector also plays a crucial role in the analysis of wave interference and the design of photonic devices.

Today, the wavevector is a standard concept taught in physics and engineering curricula worldwide, and it is routinely used in research and industry. Organizations such as the American Physical Society and the Institute of Physics provide resources and publications that further explore the applications and implications of the wavevector in contemporary science and technology.

Mathematical Foundations: Representing Waves with Vectors

The wavevector is a fundamental concept in the mathematical representation of waves, particularly in physics and engineering. It provides a compact and precise way to describe both the direction and the spatial frequency of a wave. Mathematically, the wavevector is denoted by the symbol k and is defined as a vector quantity whose magnitude is related to the wavelength (λ) of the wave by the relation |k| = 2π/λ. The direction of the wavevector indicates the direction in which the wave propagates.

In the context of a plane wave, the wave can be represented as a function of position and time using the expression:

  • ψ(r, t) = A exp[i(k · r − ωt)]

where ψ is the wave function, A is the amplitude, r is the position vector, ω is the angular frequency, and t is time. The dot product k · r ensures that the phase of the wave advances in the direction of propagation. This formalism is widely used in fields such as quantum mechanics, optics, and acoustics to analyze wave phenomena.

The wavevector plays a crucial role in the study of wave interference, diffraction, and the propagation of waves in different media. For example, in crystallography, the concept of the reciprocal lattice is built upon the wavevector, enabling the analysis of X-ray diffraction patterns and the determination of crystal structures. In quantum mechanics, the wavevector is directly related to the momentum of a particle through the de Broglie relation, p = ħk, where ħ is the reduced Planck constant. This relationship underpins the wave-particle duality central to modern physics, as described by organizations such as the American Physical Society.

Furthermore, the wavevector formalism is essential in the study of electromagnetic waves, as outlined by the Institute of Electrical and Electronics Engineers (IEEE). In these contexts, the wavevector not only determines the direction of energy flow but also interacts with material properties, such as refractive index, to influence phenomena like refraction and reflection.

In summary, the wavevector provides a mathematically rigorous and physically meaningful way to represent waves, encapsulating both their spatial periodicity and directionality. Its applications span multiple scientific disciplines, making it a cornerstone of wave theory and analysis.

Wavevector in Quantum Mechanics: Momentum and Uncertainty

In quantum mechanics, the concept of the wavevector is fundamental to understanding the behavior of particles at microscopic scales. The wavevector, typically denoted as k, is a vector quantity that characterizes the spatial frequency of a wave associated with a quantum particle. It is directly related to the wavelength (λ) of the particle’s wavefunction by the relation k = 2π/λ. The direction of the wavevector indicates the direction of wave propagation, while its magnitude is inversely proportional to the wavelength.

The wavevector plays a crucial role in connecting the wave-like and particle-like properties of matter, as described by the de Broglie hypothesis. According to this principle, every particle with momentum p can be associated with a wave whose wavevector is given by p = ħk, where ħ is the reduced Planck constant. This relationship forms the basis for the mathematical description of quantum states in terms of plane waves and underpins the formalism of quantum mechanics, including the Schrödinger equation.

The wavevector is also central to the formulation of the Heisenberg uncertainty principle. In quantum mechanics, the position and momentum of a particle cannot both be precisely determined; their uncertainties are inversely related. Since momentum is proportional to the wavevector, uncertainty in the wavevector (Δk) is directly linked to uncertainty in momentum (Δp). The uncertainty principle can thus be expressed as Δx · Δk ≥ 1/2, where Δx is the uncertainty in position. This relationship highlights the intrinsic limitations in simultaneously measuring a particle’s position and its associated wavevector, reflecting the fundamental probabilistic nature of quantum systems.

In practical terms, the wavevector is essential in analyzing phenomena such as diffraction, interference, and the electronic properties of solids. For example, in solid-state physics, the wavevector is used to describe the quantum states of electrons in a crystal lattice, leading to the concept of energy bands and the Brillouin zone. The precise manipulation and measurement of wavevectors are critical in technologies such as electron microscopy and semiconductor device engineering.

The rigorous mathematical treatment of wavevectors and their implications for momentum and uncertainty is foundational to modern quantum theory, as established by pioneering work from organizations such as the American Physical Society and the Institute of Physics, which continue to advance research and education in quantum mechanics.

Role in Crystallography and Solid-State Physics

In crystallography and solid-state physics, the concept of the wavevector is fundamental to understanding the behavior of waves—particularly electrons and phonons—within periodic structures such as crystals. The wavevector, often denoted as k, is a vector quantity that characterizes both the direction and the wavelength (or equivalently, the momentum) of a wave propagating through a medium. Its magnitude is inversely proportional to the wavelength, and its direction indicates the direction of wave propagation.

In the context of crystals, the periodic arrangement of atoms leads to the formation of a reciprocal lattice, a mathematical construct that simplifies the analysis of wave phenomena in periodic systems. The wavevector is central to this framework, as it allows for the description of electron states and vibrational modes (phonons) using Bloch’s theorem. According to Bloch’s theorem, the wavefunctions of electrons in a periodic potential can be expressed as a plane wave modulated by a function with the periodicity of the lattice. The wavevector k thus serves as a quantum number labeling these states, and its values are typically confined to the first Brillouin zone, a uniquely defined region in reciprocal space.

The role of the wavevector extends to the analysis of electronic band structures, which are crucial for determining the electrical, optical, and thermal properties of materials. The relationship between the energy of an electron and its wavevector (the E–k relation) reveals the allowed and forbidden energy bands in a crystal, dictating whether a material behaves as a conductor, semiconductor, or insulator. Similarly, the dispersion relations for phonons—quantized lattice vibrations—are described as functions of the wavevector, providing insight into thermal conductivity and other vibrational properties.

Experimental techniques such as X-ray diffraction and neutron scattering rely on the concept of the wavevector to interpret the interaction of incident waves with the crystal lattice. The change in wavevector during these interactions provides information about the crystal structure, atomic positions, and dynamic processes within the material. Organizations such as the International Union of Crystallography and the American Physical Society play key roles in advancing research and standardizing methodologies in these fields.

In summary, the wavevector is an indispensable tool in crystallography and solid-state physics, underpinning the theoretical description and experimental investigation of wave phenomena in periodic solids.

Wavevector and Dispersion Relations: Understanding Wave Propagation

The wavevector is a fundamental concept in the study of wave phenomena, serving as a vector quantity that characterizes both the direction and the spatial frequency of a wave. Mathematically, the wavevector, often denoted as k, is defined as the gradient of the phase of the wave, and its magnitude is inversely proportional to the wavelength. In three-dimensional space, the wavevector provides a concise description of how the phase of a wave varies in space, with its direction indicating the direction of wave propagation and its length given by ( |k| = 2pi/lambda ), where ( lambda ) is the wavelength.

The importance of the wavevector extends across various branches of physics, including optics, acoustics, and quantum mechanics. In optics, for example, the wavevector is central to the analysis of light propagation, refraction, and diffraction. It is also crucial in the study of electromagnetic waves, as described by Maxwell’s equations, where the wavevector helps determine the behavior of light in different media. The Optica (formerly Optical Society of America) is a leading organization in the field of optics and photonics, providing resources and standards for the study and application of wave phenomena.

In solid-state physics, the wavevector plays a pivotal role in describing the behavior of electrons and phonons in crystalline materials. The concept of the Brillouin zone, for instance, is defined in terms of the wavevector and is essential for understanding electronic band structures. The American Physical Society is a prominent authority in advancing research and education in physics, including the study of wavevectors in condensed matter systems.

The wavevector is also intimately connected to the concept of momentum in quantum mechanics. According to the de Broglie hypothesis, the momentum of a particle is directly proportional to its wavevector, ( p = hbar k ), where ( hbar ) is the reduced Planck constant. This relationship underpins much of modern quantum theory and is foundational in the analysis of wave-particle duality.

Overall, the wavevector serves as a unifying parameter in the mathematical description of waves, enabling the analysis of wave propagation, interference, and dispersion in a wide range of physical systems. Its utility is evident in both theoretical frameworks and practical applications, making it a cornerstone of modern physics and engineering.

Applications in Optics and Photonics

The concept of the wavevector is fundamental in optics and photonics, serving as a cornerstone for understanding the propagation, interaction, and manipulation of light in various media. The wavevector, typically denoted as k, is a vector quantity that describes both the direction of propagation and the spatial frequency (wavelength) of a wave. Its magnitude is inversely proportional to the wavelength, and its direction indicates the direction of energy flow. In optics and photonics, the wavevector is crucial for analyzing phenomena such as refraction, diffraction, interference, and the behavior of light in complex materials.

One of the primary applications of the wavevector in optics is in the analysis of light propagation through different media. According to Optica (formerly OSA), the change in the wavevector at the interface between two materials with different refractive indices underpins Snell’s Law, which governs the refraction of light. The conservation of the parallel component of the wavevector at boundaries is essential for predicting how light bends or reflects at surfaces, a principle widely used in lens design, fiber optics, and photonic devices.

In photonics, the wavevector is central to the study of photonic crystals and metamaterials. These engineered structures manipulate the propagation of light by creating periodic variations in refractive index, leading to the formation of photonic band gaps—frequency ranges where light cannot propagate. The relationship between the wavevector and frequency, described by the photonic band structure, determines the allowed and forbidden modes of light within these materials. This principle is harnessed in the development of highly efficient waveguides, optical filters, and devices for controlling spontaneous emission, as highlighted by research from organizations such as Massachusetts Institute of Technology (MIT).

Wavevector analysis is also vital in the field of nonlinear optics, where the phase-matching condition—requiring the sum of the wavevectors of interacting photons to be conserved—enables efficient frequency conversion processes like second-harmonic generation and parametric amplification. This underpins the operation of many modern laser systems and quantum light sources, as described by SPIE, the international society for optics and photonics.

Furthermore, the wavevector formalism is indispensable in the design and analysis of optical communication systems, where understanding the dispersion and propagation of light pulses in optical fibers is critical for high-speed data transmission. The wavevector’s role in describing modal propagation and dispersion relations ensures the optimization of bandwidth and signal integrity in global telecommunication networks.

Wavevector in Computational Simulations and Modeling

In computational simulations and modeling, the concept of the wavevector is fundamental for describing and analyzing periodic phenomena, especially in fields such as condensed matter physics, materials science, and computational chemistry. The wavevector, typically denoted as k, characterizes the spatial frequency and direction of a wave, and is central to the mathematical representation of waves in both real and reciprocal (momentum) space. In simulations, the wavevector is crucial for interpreting the results of techniques such as molecular dynamics, density functional theory (DFT), and lattice dynamics.

One of the primary uses of the wavevector in computational modeling is in the analysis of periodic boundary conditions. When simulating a finite portion of a material, periodic boundary conditions are often applied to mimic an infinite system. The allowed wavevectors in such a system are quantized according to the size and shape of the simulation cell, and these discrete k-points are used to sample the Brillouin zone in reciprocal space. This sampling is essential for calculating properties such as electronic band structures, phonon dispersion relations, and optical spectra. The accuracy of these calculations depends on the density and distribution of the sampled wavevectors.

In electronic structure calculations, such as those performed using DFT, the wavevector is used to label the electronic states in crystalline solids. The electronic energy bands are functions of the wavevector, and their dispersion relations provide insight into the conductive, semiconductive, or insulating nature of materials. Computational packages like Quantum ESPRESSO and VASP (Vienna Ab initio Simulation Package) implement sophisticated algorithms for k-point sampling, enabling efficient and accurate modeling of electronic properties.

Similarly, in lattice dynamics and phonon calculations, the wavevector describes the collective vibrational modes of atoms in a crystal. The phonon dispersion relations, which plot vibrational frequencies as a function of the wavevector, are critical for understanding thermal conductivity, specific heat, and other thermodynamic properties. Tools such as Phonopy are widely used for these purposes, leveraging the wavevector formalism to compute and visualize phonon spectra.

Overall, the wavevector serves as a bridge between real-space atomic configurations and reciprocal-space representations of physical phenomena. Its role in computational simulations is indispensable for predicting and interpreting the properties of materials at the atomic and electronic levels, making it a cornerstone concept in modern computational science.

Experimental Techniques for Measuring Wavevectors

The measurement of wavevectors is fundamental in experimental physics, particularly in fields such as condensed matter physics, optics, and materials science. The wavevector, typically denoted as k, characterizes the direction and magnitude of a wave’s propagation and is directly related to its wavelength and frequency. Accurate determination of wavevectors enables the analysis of phenomena such as diffraction, interference, and the electronic structure of materials.

One of the most widely used experimental techniques for measuring wavevectors is X-ray diffraction (XRD). In XRD, a monochromatic X-ray beam is directed at a crystalline sample, and the angles and intensities of the diffracted beams are measured. The positions of the diffraction peaks correspond to specific wavevectors, which are determined using Bragg’s law. This technique is essential for elucidating crystal structures and is standardized by organizations such as the International Union of Crystallography.

Another important method is neutron scattering, which is particularly valuable for probing magnetic structures and dynamics in materials. Neutron beams, due to their neutral charge and suitable wavelength, interact with atomic nuclei and magnetic moments, allowing for precise measurement of wavevector transfers during scattering events. Facilities like the Institut Laue-Langevin and the National Institute of Standards and Technology operate advanced neutron sources for such experiments.

In the realm of surface science, angle-resolved photoemission spectroscopy (ARPES) is a powerful technique for measuring the electronic band structure of solids. By irradiating a material with photons and analyzing the kinetic energy and emission angle of the ejected electrons, researchers can reconstruct the electrons’ initial wavevectors within the crystal. This method is crucial for studying phenomena such as superconductivity and topological insulators, and is supported by research at major synchrotron facilities, including the European Synchrotron Radiation Facility.

For optical waves, Fourier transform spectroscopy and interferometry are commonly employed. These techniques analyze the spatial and temporal coherence of light to extract wavevector information, which is vital in photonics and optical engineering. Organizations such as the Optica (formerly OSA) provide resources and standards for these measurements.

In summary, the choice of experimental technique for measuring wavevectors depends on the type of wave (X-ray, neutron, electron, or photon) and the specific properties of the material or system under investigation. The continued development and refinement of these methods are central to advances in both fundamental and applied science.

Wavevector in Emerging Technologies: Nanoscience and Metamaterials

The concept of the wavevector is central to the understanding and advancement of emerging technologies, particularly in the fields of nanoscience and metamaterials. The wavevector, typically denoted as k, characterizes the direction and magnitude of wave propagation in a medium. In nanoscience, where materials and devices are engineered at the atomic and molecular scale, the wavevector is crucial for describing phenomena such as electron transport, phonon dynamics, and light-matter interactions. For instance, in quantum wells, wires, and dots, the quantization of the wavevector due to spatial confinement leads to discrete energy levels, fundamentally altering the electronic and optical properties of nanostructures. This underpins the operation of nanoscale transistors, quantum dots, and other devices that form the backbone of modern nanotechnology (National Nanotechnology Initiative).

In the realm of metamaterials—artificially structured materials engineered to exhibit properties not found in nature—the wavevector plays a pivotal role in determining how electromagnetic waves interact with these materials. Metamaterials are designed to manipulate the wavevector of light, enabling phenomena such as negative refraction, cloaking, and superlensing. By tailoring the periodicity and geometry of the constituent elements at subwavelength scales, researchers can control the effective wavevector within the material, leading to novel optical and electromagnetic responses. This has significant implications for the development of advanced imaging systems, sensors, and communication devices (Optica (formerly Optical Society of America)).

Furthermore, the study of wavevector-dependent phenomena is essential for the design of photonic and phononic crystals, which are periodic structures that affect the propagation of photons and phonons, respectively. The band structure of these crystals, determined by the allowed and forbidden wavevectors, enables the control of light and sound at the nanoscale. This capability is being harnessed for applications ranging from efficient light-emitting diodes to novel thermal management systems (IEEE).

As nanoscience and metamaterials continue to evolve, the precise manipulation and understanding of the wavevector remain at the forefront of research and technological innovation. The ability to engineer wavevector-dependent properties is opening new frontiers in information processing, energy harvesting, and beyond, underscoring the foundational role of this concept in the next generation of advanced materials and devices.

Future Directions: Challenges and Opportunities in Wavevector Research

The study of wavevectors—quantities that describe both the direction and magnitude of wave propagation—remains central to advancements in physics, materials science, and engineering. As research delves deeper into complex systems, several challenges and opportunities are emerging that will shape the future of wavevector-related investigations.

One of the primary challenges lies in the precise measurement and manipulation of wavevectors in increasingly complex and miniaturized systems. In nanophotonics and quantum materials, for example, the ability to resolve and control wavevectors at the atomic or sub-wavelength scale is crucial for the development of next-generation devices. Techniques such as angle-resolved photoemission spectroscopy (ARPES) and advanced electron microscopy are being refined to address these needs, but limitations in spatial and energy resolution persist. Overcoming these barriers will require continued innovation in instrumentation and experimental methodologies, as highlighted by leading research institutions such as the Lawrence Berkeley National Laboratory and the Max Planck Society.

Another significant opportunity is the exploration of wavevector-dependent phenomena in novel materials, such as topological insulators, 2D materials, and metamaterials. These systems exhibit unique electronic, optical, and acoustic properties that are fundamentally governed by their wavevector-dependent band structures. Understanding and harnessing these properties could lead to breakthroughs in quantum computing, energy harvesting, and information processing. Organizations like the National Institute of Standards and Technology (NIST) are actively developing standards and measurement techniques to support this research frontier.

Computational modeling and simulation also present both challenges and opportunities. Accurately predicting wavevector-dependent behavior in large, disordered, or strongly correlated systems requires significant computational resources and sophisticated algorithms. Advances in high-performance computing, machine learning, and data-driven approaches are beginning to address these challenges, enabling researchers to explore previously inaccessible regimes of wavevector space.

Looking ahead, interdisciplinary collaboration will be essential. Progress in wavevector research will depend on the integration of expertise from physics, materials science, engineering, and computer science. International organizations such as the American Physical Society and the International Union of Crystallography play a pivotal role in fostering such collaborations, organizing conferences, and disseminating best practices.

In summary, while significant technical and conceptual challenges remain, the future of wavevector research is rich with opportunities. Continued investment in experimental techniques, computational tools, and collaborative networks will be key to unlocking the full potential of wavevector-driven phenomena in science and technology.

Sources & References

Unlocking Quantum Power The Multiverse Explained!

Leave a Reply

Your email address will not be published. Required fields are marked *