Recent News

שחרור כוח הווקטור גלים: המפתח להבנות קוונטריות וחומריות

Posted on
Unlocking the Power of Wavevector: The Key to Quantum and Material Insights

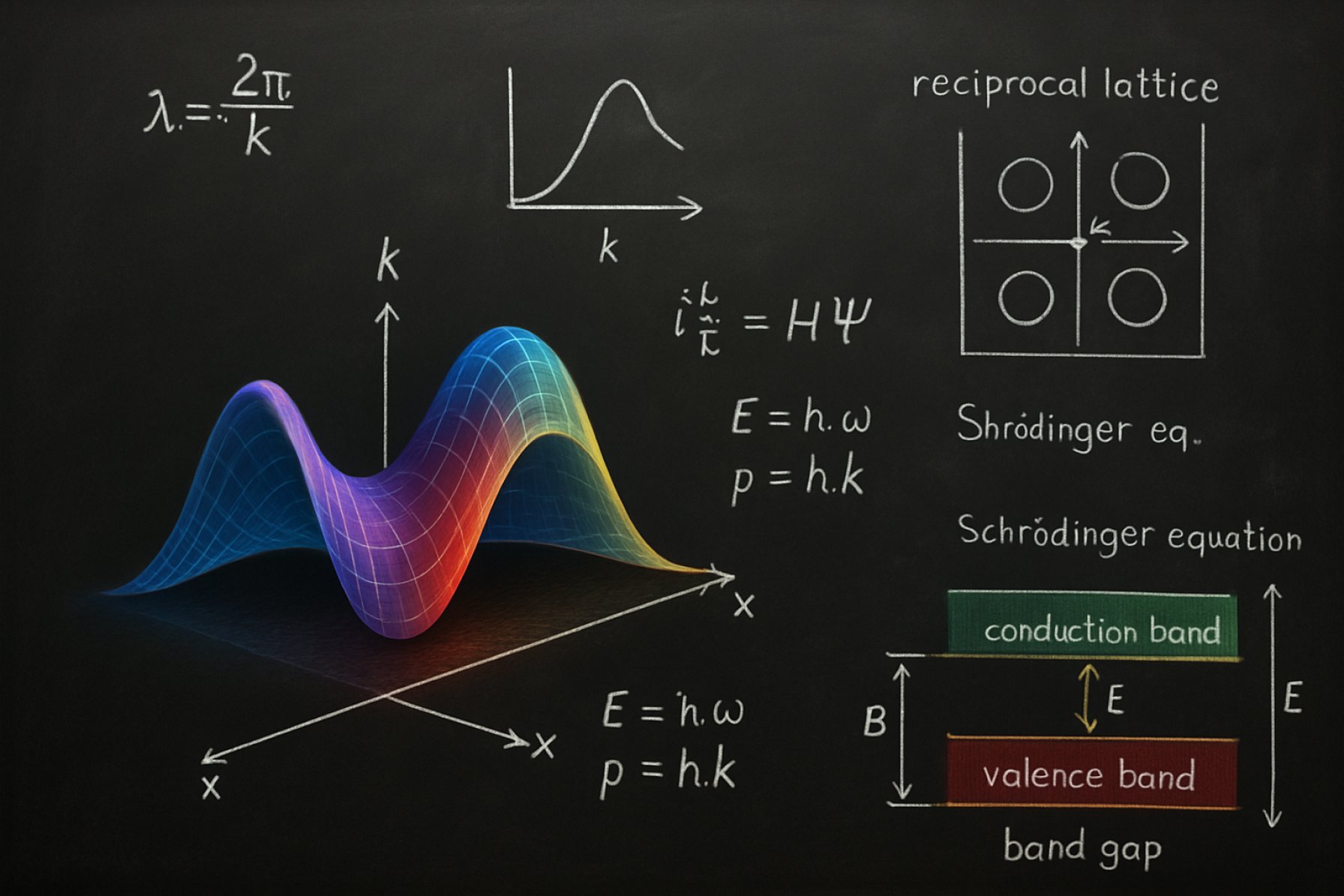
וקטור גלים ממוסד: כיצד הקונספט הבסיסי הזה מעצב פיזיקה קוונטית, מדע חומרים ועוד. גלה את הדפוסים הנסתרים ששולטים בגלים ובחלקיקים.

מבוא לוקטור גלים: הגדרה והקשר היסטורי

המושג של וקטור גלים הוא יסודי בלימוד תופעות גלים ברחבי הפיזיקה, כולל אופטיקה, אקוסטיקה ומכניקת קוונטים. וקטור גלים, בדרך כלל מסומן על ידי הסימן k, הוא כמות וקטורית שמתארת הן את כיוון התפשטות והן את התדר המרחבי של גל. מתמטית, המידה של וקטור הגלים ניתנת על ידי ( |k| = 2pi/lambda ), כאשר ( lambda ) הוא אורך הגל. כיוון הווקטור מצביע בכיוון שבו הגל מתפשט. תפקיד זה הופך את וקטור הגלים לכלי מרכזי בתיאור תופעות מחזוריות, כגון גלים אלקטרומגנטיים, גלי קול ופונקציות גל של חלקיקים במכניקת קוונטים.

במובן ההיסטורי, המושג וקטור גלים התפתח מתוך הפיתוח של תיאור תופעות גלים במאה ה-19, במיוחד כאשר מדענים ניסו לתאר מתמטית את האור והקול כגלים. הפורמליזציה של וקטור הגלים הייתה קשורה מאוד להופעת אנליזת פורייה, שהאפשרה לפרק צורות גלים מורכבות לסכומים של רכיבי סינוסואידיים, כל אחד מהם מאופיין בווקטור גל ספציפי. בהקשר של קריסטלוגרפיה ופיזיקה של מצב מוצק, וקטור הגלים הפך במיוחד לחשוב בתיאור התנהגות של אלקטרונים ופונונים בגרעינים מחזוריים, כפי שנראה בפיתוח תיאוריה של מסילות ואזורי ברילואן.

בעידן המודרני, וקטור הגלים הוא הכרחי. במכניקת קוונטים, לדוגמה, וקטור הגלים קשור ישירות לתנע של חלקיק באמצעות הקשר דה ברולי ( p = hbar k ), כאשר ( hbar ) הוא הקבוע פלנק המופחת. קשר זה עומד מאחורי רבים מהתיאוריות הקוונטיות והוא בסיסי בלימוד התנהגות של אלקטרונים בחומרים. באופטיקה, וקטור הגלים מתאר את התפשטות האור במדיות שונות, משפיע על תופעות כגון השבירה וההפרעה. וקטור הגלים גם משחק תפקיד חיוני בהבנה של התערבות גלים ובעיצוב מכשירים פוטוניים.

היום, וקטור הגלים הוא מושג סטנדרטי הנלמד בתוכניות פיזיקה והנדסה בכל העולם, והוא משמש באופן שגרתי במחקר ובתעשייה. ארגונים כמו החברה האמריקאית לפיזיקה והמכון לפיזיקה מספקים משאבים ופרסומים שמעמיקים את הבנת וקטור הגלים ביישומים ובמשמעויותיו במדע ובטכנולוגיה המודרנית.

יסודות מתמטיים: ייצוג גלים עם וקטורים

וקטור הגלים הוא מושג בסיסי בייצוג מתמטי של גלים, במיוחד בתחום הפיזיקה וההנדסה. הוא מספק דרך קומפקטית ומדויקת לתאר הן את הכיוון והן את התדר המרחבי של גל. מתמטית, וקטור הגלים מסומן על ידי הסימן k ומוגדר ככמות וקטורית שמידה שלה קשורה לאורך הגל (λ) של הגל באמצעות הקשר |k| = 2π/λ. כיוון וקטור הגלים מצביע על הכיוון שבו הגל מתפשט.

בהקשר של גל מישורי, ניתן לייצג את הגל כפונקציה של מיקום וזמן באמצעות הביטוי:

  • ψ(r, t) = A exp[i(k · r − ωt)]

כאשר ψ היא פונקציית הגל, A היא האמפליטודה, r הוא וקטור המיקום, ω היא התדר הזוויתי, ו-t הוא הזמן. מכפלה הסקלרית k · r מבטיחה שהשלב של הגל מתקדמת בכיוון התפשטות. פורמליזם זה נמצא בשימוש נרחב בתחומים כמו מכניקת קוונטים, אופטיקה ואקוסטיקה לניתוח תופעות גלים.

וקטור הגלים משחק תפקיד מרכזי בלימוד התערבות גלים, הפרעה והתפשטות גלים במדיות שונות. לדוגמה, בקריסטלוגרפיה, המושג של הרשת ההפוכה מבוסס על וקטור הגלים, ומאפשר ניתוח של דפוסי פיזור קרני רנטגן וקביעת מבני גבישים. במכניקת קוונטים, וקטור הגלים קשור ישירות לתנע של חלקיק דרך הקשר דה ברולי, p = ħk, כאשר ħ הוא הקבוע פלנק המופחת. קשר זה עומד מאחורי הדואליות של גל-חלקיק שהינה מרכזית לפיזיקה המודרנית, כפי שמתואר על ידי ארגונים כמו החברה האמריקאית לפיזיקה.

יתרה מכך, הפורמליזם של וקטור הגלים הוא חיוני בלימוד גלים אלקטרומגנטיים, כפי שמתוארת על ידי המכון למהנדסי חשמל ואלקטרוניקה (IEEE). בהקשרים אלו, וקטור הגלים לא רק קובע את כיוון זרימת האנרגיה אלא גם אינטראקציות עם תכונות חומריות, כגון מדד השבירה, להשפיע על תופעות כמו השבירה והחזרה.

לסיכום, וקטור הגלים מספק דרך מתמטית מחמירה ופיזית משמעותית לייצוג גלים, encapsulating both their spatial periodicity and directionality. Its applications span multiple scientific disciplines, making it a cornerstone of wave theory and analysis.

וקטור גלים במכניקת קוונטים: תנע וחוסר ודאות

במכניקת קוונטים, המושג של וקטור הגלים הוא יסודי להבנת התנהגות של חלקיקים בקנה מידה מיקרוסקופי. וקטור הגלים, בדרך כלל מסומן כk, הוא כמות וקטורית שמתארת את התדר המרחבי של גל הקשור לחלקיק קוונטי. הוא קשור ישירות לאורך הגל (λ) של פונקציית הגל של החלקיק באמצעות הקשר k = 2π/λ. כיוון וקטור הגלים מצביע על כיוון התפשטות הגל, בעוד שמידתו הפוכה לאורך הגל.

וקטור הגלים משחק תפקיד מרכזי בחיבור בין תכונות הגלים והחלקיקים של החומר, כפי שמתואר על ידי ההיפותזה של דה ברולי. לפי עיקרון זה, כל חלקיק עם תנע p ניתן לקשר עם גל, שלוקטור הגלים שלו נתון על ידי p = ħk, כאשר ħ הוא הקבוע פלנק המופחת. קשר זה מהווה את הבסיס לתיאור המתמטי של מצבים קוונטיים מבחינת גלים מישורים ומחזק את הפורמליזם של מכניקת קוונטים, כולל את משוואת שרדינגר.

וקטור הגלים הוא גם מרכזי בניסוח של עקרון חוסר הוודאות של הייזנברג. במכניקת קוונטים, מיקום ותנע של חלקיק לא יכולים להתקיים בדיוק; חוסר הוודאות שלהם מתייחס ההפוכה. שכן התנע פרופורציונלי לוקטור הגלים, חוסר הוודאות בוקטור הגלים (Δk) מחובר ישירות לחוסר הוודאות בתנע (Δp). עקרון חוסר הוודאות ניתן להביע כך: Δx · Δk ≥ 1/2, כאשר Δx הוא חוסר הוודאות במיקום. קשר זה מדגיש את ההגבלות הפנימיות במדידת מיקום החלקיק ווקטור גלים הקשור בו זמנית, משקף את הטבע הסיכומי הבסיסי של מערכות קוונטיות.

במונחים מעשיים, וקטור הגלים חיוני לניתוח תופעות כמו הפרעה, התפשטות והתנהגות אלקטרונית של חומרים. לדוגמה, בפיזיקה של מצב מוצק, וקטור הגלים משמש לתיאור מצבים קוונטיים של אלקטרונים בגרעין גביש, leading to the concept of energy bands and the Brillouin zone. ההתמודדות המדויקת עםמדידה של וקטורי גלים היא קריטית באמצעים כמו מיקרוסקופיית אלקטרונים והנדסת מכשירים מבוססי חצי מוליך.

הטיפול המתמטי המדויק של וקטורי גלים והמשמעויות שלהם לתנע וחוסר ודאות הוא בסיסי לתיאוריה הקוונטית המודרנית, כפי שהוקם בעבודות חלוציות מארגונים כמו החברה האמריקאית לפיזיקה והמכון לפיזיקה, הממשיכים לקדם מחקר וחינוך במכניקת קוונטים.

תפקיד בקריסטלוגרפיה ופיזיקה של מצב מוצק

בקריסטלוגרפיה ובפיזיקה של מצב מוצק, המושג של וקטור הגלים הוא יסודי להבנה של התנהגות גלים—בפרט אלקטרונים ופונונים—בתוך מבנים מחזוריים כמו גבישים. וקטור הגלים, שמסומן לרוב על ידי k, הוא כמות וקטורית שמתארת הן את הכיוון והן את אורך הגל (או באופן שקול, את התנע) של גל המתפשט באמצעות חומר. מידתו הפוכה לאורך הגל, וכיוונו מצביע על כיוון התפשטות הגל.

בהקשר של גבישים, הסידור המחזורי של אטומים מוביל להיווצרות של רשת הפוכה, מבנה מתמטי המקל על הניתוח של תופעות גלים במערכות מחזוריות. וקטור הגלים הוא מרכזי במסגרת זו, שכן הוא מאפשר לתאר מצבים אלקטרוניים ומודוסים תנודתיים (פונונים) באמצעות משפט בלוך. לפי משפט בלוך, פונקציות הגל של אלקטרונים במתח מחזורי יכולות להיות מבוטאות כגל מישורי המוזן על ידי פונקציה עם מחזוריות של הרשת. וקטור הגלים k משמש לפיכך כמספר קוונטי המסמן את המצבים הללו, ולערכיו בדרך כלל יש מגבלה לאזור ברילואן הראשון, אזור מוגדר באופן ייחודי במרחב ההפוך.

תפקיד הווקטור הגלים מתרחב לניתוח של מבני באנדים אלקטרוניים, שהם קריטיים לקביעת התכונות החשמליות, האופטיות והתרמיות של חומרים. הקשר בין האנרגיה של אלקטרון ווקטור הגלים שלו (קשר E–k) חושף את הבאנדים האנרגטיים המותרים והאסורים בגביש, קובע אם חומר מתנהג כמוליך, חצי מוליך או מבודד. באופן דומה, יחסי הפיזור לפונונים—תנודות לattice כמותיות—מתוארים כפונקציות של וקטור הגלים, מספקים תובנות לגבי מוליכות תרמית ותכונות תנודתיות אחרות.

טכניקות ניסיוניות כמו פיזור קרני רנטגן ופיזור ניוטרונים מסתמכות על המושג של וקטור הגלים כדי לפרש את האינטראקציה של גלים חודרים עם הרשת הגבוית. השינוי בוקטור הגלים במהלך אינטראקציות אלו מספק מידע על מבנה הגביש, מיקומי אטומים ותהליכים דינמיים בתוך החומר. ארגונים כמו האיגוד הבינלאומי לקריסטלוגרפיה והחברה האמריקאית לפיזיקה משחקים תפקיד מרכזי בהקניית מחקר ובסטנדרטיזציה של שיטות עבודה בתחומים אלו.

לסיכום, וקטור הגלים הוא כלי שאין לו תחליף בקריסטלוגרפיה ובפיזיקה של מצב מוצק, המספק את התיאור התיאורטי והמחקרי של תופעות גלים במוצקים מחזוריים.

וקטור גלים ויחסי פיזור: הבנת התפשטות גלים

וקטור הגלים הוא מושג בסיסי בלימוד תופעות גלים, המשמש ככמות וקטורית שמתארת הן את הכיוון והן את התדר המרחבי של גל. מתמטית, וקטור הגלים, שנקרא לרוב k, מוגדר כגרדיאנט של השלב של הגל, ומידתו הפוכה לאורך הגל. במרחב תלת-ממדי, וקטור הגלים מספק תיאור תמציתי של איך השלב של גל משתנה במרחב, כאשר הכיווניות מציינת את כיוון התפשטות הגל ואורכו ניתן על ידי ( |k| = 2pi/lambda ), בתנא חשבי ( lambda ) מהווה את אורך הגל.

חשיבותו של וקטור הגלים מתפרסת על פני ענפי פיזיקה שונים, כולל אופטיקה, אקוסטיקה ומכניקת קוונטים. באופטיקה, לדוגמה, וקטור הגלים הוא מרכזי לניתוח התפשטות אור, השבירה וההפרעה. הוא גם חיוני בלימוד גלים אלקטרומגנטיים, כפי שמתואר על ידי משוואות מקסוול, שם וקטור הגלים מסייע לקבוע את התנהגות האור במדיות שונות. הOptica (לשעבר האגודה האופטית של אמריקה) היא ארגון מוביל בתחום האופטיקה והפוטוניקה, המספק משאבים ותקנים ללימוד וליישום תופעות גלים.

בפיזיקה של מצב מוצק, וקטור הגלים משחק תפקיד חשוב בתיאור התנהגות של אלקטרונים ופונונים בחומרים גבישיים. המושג של אזור ברילואן, למשל, מוגדר במונחים של וקטור הגלים והוא חיוני להבנת מבני באנדים אלקטרוניים. החברה האמריקאית לפיזיקה היא סוכנות בולטת בתמיכה במחקר ובחינוך בפיזיקה, כולל לימוד וקטורי גלים במערכות מצב ממושך.

וקטור הגלים גם קשור באופן אינטימי למושג התנע במכניקת קוונטים. בהתאם להיפותזה של דה ברולי, התנע של חלקיק פרופורציונלי ישירות לוקטור הגלים שלו, ( p = hbar k ), כאשר ( hbar ) הוא הקבוע פלנק המופחת. קשר זה עומד מאחורי רבים מהתיאוריות הקוונטיות המודרניות והוא בסיסי לניתוח הדואליות של גל-חלקיק.

באופן כללי, וקטור הגלים משמש כפרמטר מאחד בתיאור המתמטי של גלים, המאפשר ניתוח של התפשטות גלים, התערבות ופיזור במגוון רחב של מערכות פיזיקליות. השימושיות שלו ניכרת הן במסגרת תיאורטית והן ביישומים מעשיים, מה שהופך את זה לאבן פינה של פיזיקה והנדסה מודרניות.

יישומים באופטיקה ופוטוניקה

המושג של וקטור הגלים הוא יסודי באופטיקה ופוטוניקה, ושימש כבסיס להבנה של התפשטות, אינטראקציה ומניפולציה של אור במדיות שונות. וקטור הגלים, בדרך כלל מסומן על ידי k, הוא כמות וקטורית שמתארת הן את כיוון התפשטות והן את התדר המרחבי (אורך גל) של גל. מידתו הפוכה לאורך הגל, וכיוונו מצביע על اتجاه זרימת האנרגיה. באופטיקה ובפוטוניקה, וקטור הגלים חיוני לניתוח תופעות כמו השבירה, הפרעה, התערבות והתנהגות של אור בחומרים מורכבים.

אחת מהיישומים העיקריים של וקטור הגלים באופטיקה היא בניתוח התפשטות אור דרך מדיות שונות. לפי הOptica (לשעבר OSA), השינוי בווקטור הגלים בנקודת המפגש בין שני חומרים עם מדדי שבירה שונים מהווה את הבסיס לחוק של סנל, המנהל את השבירה של אור. השימור של הרכיב המקביל של וקטור הגלים בגבולות הוא חיוני לחיזוי כיצד אור מתעקם או מוחזר על פני משטחים, עקרון שמשמש מאוד בעיצוב עדשות, אופטיקה סיבית ומכשירים פוטוניים.

בפוטוניקה, וקטור הגלים הוא מרכזי בלימוד גבישי פוטונים ומטמטמטרים. מבנים אלו, המעוצבים, מניפולצים את התפשטות האור על ידי יצירת שינויים מחזוריים במדדי השבירה, ויוצרים את התהוות הבנדים הפוטוניים—טווחי תדרים שבהם אור לא יכול להתפשט. הקשר בין וקטור הגלים ותדר, המתואר על ידי מבנה בנד פוטוניים, קובע את המודוסים המותרים והאסורים של אור בחומרים אלו. עיקרון זה מנוצל בפיתוח גיוני אור יעילים במיוחד, מסננים אופטיים ומכשירים לשליטה בפליטה ספונטנית, כפי שהודגש על ידי מחקר מארגונים כמו המכון הטכנולוגי של מסצ'וסטס (MIT).

ניתוח וקטורי גלים גם חיוני בתחום האופטיקה הלא ליניארית, שבו תנאי ההתאמה של השלב—שדורש שהסכום של וקטורי הגלים של פוטונים אינטראקציה יישמר—מאפשר תהליכי המרה תדרים יעילים כמו ייצור שניוני ותגבור פרמטרי. זה עומד מאחורי הפעולה של רבים ממערכות הלייזר המודרניות ומקורות אור קוונטיים, כפי שמתואר על ידי SPIE, האגודה הבינלאומית לאופטיקה ופוטוניקה.

יתרה מכך, הפורמליזם של וקטור הגלים הוא חיוני בעיצוב וניתוח מערכות תקשורת אופטיות, שם הבנת הפיזור והתפשטות של פולסי אור באופטיקה סיבית היא קריטית להעברת נתונים במהירות גבוהה. תפקידו של וקטור הגלים בתיאור הפצת מודלים ויחסי פיזור מבטיח את אופטימיזציה של רוחב פס ושלמות האות ברשתות התקשורת הגלובליות.

וקטור גלים בסימולציות חישוביות וד modeling

בסיומות חישוביות וד modeling, המושג של וקטור הגלים הוא יסודי לתיאור ולניתוח תופעות מחזוריות, במיוחד בתחומים כמו פיזיקה של מצב מוצק, מדע חומרים וכימיה חישובית. וקטור הגלים, שמסומן בדרך כלל כk, מתאר את התדר המרחבי ואת כיוון של גל, והוא חיוני לייצוג המתמטי של גלים בשני המרחבים הממשיים וההפוכים (תנע). בסימולציות, וקטור הגלים הוא קריטי לפרשנות התוצאות של טכניקות כמו דינמיקת מולקולות, תיאוריה של פונקציית צפיפות (DFT) ודינמיקת לattice.

אחד השימושים העיקריים של וקטור הגלים במודלים חישוביים הוא בניתוח של תנאים גבול מחזוריים. כאשר מדמים חלק מסוים מחומר, לעיתים קרובות מוחלים תנאים גבול מחזוריים כדי לדמות מערכת אינסופית. וקטורי הגלים המותרים במערכת כזו הם קוונטיים לפי גודל וצורת תא הסימולציה, וk-points הללו משמשים לדגימת אזור ברילואן במרחב ההפוך. דגימה זו חיונית לחישוב תכונות כמו מבני באנדים אלקטרוניים, יחסי פיזור פונונים וספקטרות אופטיות. דיוק החישובים הללו תלוי בדחיסות ובפיזור של וקטורי הגלים המדוגמים.

בחישובי מבנה אלקטרוני, כמו אלו שנערכים באמצעות DFT, וקטור הגלים משמש לסימון מצבים אלקטרוניים בגבישים. הבנדים האנרגטיים האלקטרוניים הם פונקציות של וקטור הגלים, ויחסי הפיזור שלהם מספקים תובNaות ביחס לתכונות חשמליות, חצי-חשמליות או מבודדות של חומרים. חבילות חישוביות כמו Quantum ESPRESSO וVASP (Vienna Ab initio Simulation Package) מממשות אלגוריתמים מתקדמים לדגימת k-points, מאפשרות מודל מדויק ויעיל של תכונות אלקטרוניות.

באופן דומה, בחישובי דינמיקת פונונים, וקטור הגלים מתאר את המודוסים התנודתיים הקולקטיביים של אטומים בגביש. יחסי הפיזור של פונונים, המהווים תדרים תנודתיים כפונקציות של וקטור הגלים, הם קריטיים להבנת מוליכות תרמית, חום ספציפי ותכונות תרמודינמיות אחרות. כלים כמו Phonopy נמצאים בשימוש נרחב למטרות אלו, מנצלים את הפורמליזם של וקטור הגלים לחישוב ולויזואליזציה של ספקטרות פונונים.

לסיכום, וקטור הגלים משמש כגשר בין קונפיגורציות אטומיות במרחב ממשי לייצוגים במרחב ההפוך של תופעות פיזיקליות. תפקידו בסימולציות חישוביות הוא הכרחי בשינוי ושיפוטן של תכונות של חומרים בקנה מידה אטומי ואלקטרוני, מה שהופך אותו למושג מרכזי במדע חישובי מודרני.

טכניקות ניסיוניות למדידת וקטורי גלים

מדידת וקטורי גלים היא חיונית בפיזיקה הניסויית, במיוחד בתחומים כמו פיזיקה של מצב מוצק, אופטיקה ומדע החומרים. וקטור הגלים, שמסומן בדרך כלל כk, מתאר הן את הכיוון והן את המידה של התפשטות הגל, והוא מקושר ישירות לאורך הגל שלו ולתדירותו. קביעת וקטורי גלים מדויקים מאפשרת ניתוח של תופעות כמו פיזור, התערבות ומבניות אלקטרוניות של חומרים.

אחת מהטכניקות הניסיוניות הנפוצות ביותר למדידת וקטורי גלים היא פיזור קרני רנטגן (XRD). ב-XRD, קרן רנטגן מונוכרומטית מכוונת אל דגם גבישי, וזוויות ועצמות של קרני רנטגן מוקרנות נמדדות. מיקומי הקצוות המפולגים מתאימים לוקטורי גלים ספציפיים, שנקבעים באמצעות החוק של ברג. טכניקה זו חיונית להבהרת מבני גביש ומתקבלת על ידי ארגונים כמו האיגוד הבינלאומי לקריסטלוגרפיה.

שיטה חשובה נוספת היא פיזור ניוטרונים, שהיא particulièrement שימושית לפרופיל מבנים ומבנים דינמיים בחומרים. קרני ניוטרונים, בשל טעינתן הניטרלית ואורך הגל המתאים, אינטראקטות עם גרעיני האטום ורגעי מגנטיים, ומאפשרות מדידה מדויקת של העברות וקטורי גלים במהלך אירועי פיזור. מתקנים כמו הInstitut Laue-Langevin וההמכון הלאומי לסטנדרטים וטכנולוגיה מפעילים מקורות ניוטרונים מתקדמים לניסויים הללו.

בתחום המדע של פני השטח, ספקטרוסקופיה פוטואמיסיה בזוית (ARPES) היא טכניקה עוצמתית למדידת מבנה הבנד האלקטרוני של מוצקים. באמצעות קרינת חומר עם פוטונים וניתוח האנרגיה הקינטית וזווית ההוצאה של האלקטרונים המורמים, חוקרי יכולים לשחזר את וקטורי הגלים הראשוניים של האלקטרונים בתוך הגביש. שיטה זו היא קריטית בלימוד תופעות כמו סופר מוליכות ומבודדים טופולוגיים, ומגובה על ידי מחקר במתקני סינכרוטרון מרכזיים, כולל המתקן קרני רנטגן האירופי.

לגלים אופטיים, ספקטרוסקופיה של המרה פורייר ואינטרפרומטריה נפוצות מאוד. טכניקות אלו מנתחות את הקוהרנטיות המרחבית והזמנית של אור כדי לחלץ מידע על וקטור הגלים, שהוא חיוני בתחום הפוטוניקה והנדסה אופטית. ארגונים כמו הOptica (לשעבר OSA) מספקים משאבים וסטנדרטים למדידות אלו.

לסיכום, בחירת הטכניקה הניסיונית למדידת וקטורי גלים תלויה בסוג הגל (קרן רנטגן, ניוטרון, אלקטרון או פוטון) ובתכונות הספציפיות של החומר או המערכת הנחקרת. הפיתוח והחדשות המתמשכות של טכניקות אלו הם מרכזיים לקידום המדע הפונדמנטלי והחלופי.

וקטור גלים בטכנולוגיות מתפתחות: ננואומנות ומטמטמטרים

המושג של וקטור הגלים הוא מרכזי להבנה וקדמה של טכנולוגיות מתפתחות, במיוחד בתחומי ננואומנות ומטמטמטרים. וקטור הגלים, בדרך כלל מסומן כk, מתאר את הכיוון והמידה של התפשטות גלים במדיום. בננואומנות, שם חומרים ומכשירים מהנדסים בקנה מידה אטומי ומולקולרי, וקטור הגלים חיוני לתיאור תופעות כגון העברת אלקטרונים, דינמיקה של פונונים ואינטראקציות אור-חומר. לדוגמה, בבורות קוונטיים, חוטים ונקודות, הקונפינציה המרחבית של וקטור הגלים גורמת לרמות אנרגיה דיסקרטיות, שמשנה באופן יסודי את התכונות האלקטרוניות והאופטיות של הננואוסטרים. זה עומד מאחורי פעולת טרנזיסטורים בננואסקאלה, נקודות קוונטיות ומכשירים אחרים שמבנה את הבסיס של ננוטכנולוגיות מודרניות (המיזם הלאומי לננוטכנולוגיה).

בתחום המטמטמטרים—חומרים מעוצבים באופן מלאכותי שהם הנדסיים כדי להראות תכונות שאינן נמצאות בטבע—וקטור הגלים משחק תפקיד מרכזי בקביעת כיצד גלים אלקטרומגנטיים אינטראקטים עם חומרים אלו. מטמטמטרים מעוצבים כדי למניפולציה את וקטור הגלים של אור, ומאפשרים תופעות כגון השבירה שלילית, הסתרה וזכוכית-על. על ידי התאמת המחזוריות והגיאומטריה של היסודות המורכבים בגודל תת-גל יביא לפיקוח על וקטור הגלים האפקטיבי בתוך החומר, מה שמוביל לתגובות אופטיות ואלקטרומגנטיות חדשות. זה יש המשמעות רבה לפיתוח מערכות הדמיה מתקדמות, חיישנים ומכשירים לתקשורת (Optica (לשעבר אגודה אופטית של אמריקה)).

יתר על כך, הלימוד של תופעות תלויות וקטור גלים הוא חיוני לעיצוב גבישי פוטונים ופונונים, שהם מבנים מחזוריים שמבקרים את התפשטות של פוטונים ופונונים, בהתאמה. מבני הבנדים של גבישים אלו, הנקבעים על ידי הוקטורים המותרים והאסורים, אפשריים את השליטה באור ובקול בקנה מידה ננומטרי. יכולת זו מנוצלת ביישומים מיטביים כמו דיודות פולטות אור יעילות ועד מערכות ניהול תרמית חדשות (IEEE).

כשהטכנולוגיות של ננואומנות ומטמטמטרים ממשיכות להתפתח, החיפוש המדויק וההבנה של וקטור הגלים נשארים בחזית של מחקר וחדשנות טכנולוגית. היכולת להביא לתכונות תלויות וקטור גלים פותחות גבולות חדשים בעיבוד מידע, חילוץ אנרגיה וכדומה, מדגישות את תפקידו הבסיסי של המושג הזה בדור הבא של חומרים ומכשירים מתקדמים.

יבוא לעתיד: אתגרים והזדמנויות במחקר וקטור גלים

הסטודיות על וקטורי גלים—כמויות שמתארות הן את הכיוון והן את המידה של התפשטות גלים—נותרות מרכזיות לקידומות בפיזיקה, מדע חומרים והנדסה. ככל שהמחקר מתעמק במערכות מורכבות, מספר אתגרים והזדמנויות מתפתחים שעשויים לעצב את עתיד החקירות הקשורות לוקטור גלים.

אחד האתגרים העיקריים טמון במדידה ובמניפולציה מדויקות של וקטורי גלים במערכות שהולכות ומתרקמות להיות מורכבות ומוקטנות. בננופוטוניקה ובחומרים קוונטיים, לדוגמה, היכולת לפענח ולשלוט בוקטורי גלים בקנה מידה אטומי או תת-גל היא קריטית לפיתוח מכשירים מהדור הבא. טכניקות כמו ספקטרוסקופיה פוטואמיסיה בזוית (ARPES) ומיקרוסקופיה אלקטרונית מתקדמת נמצאות בבחינה כדי לענות על צרכים אלו, אך מגבלות ברזולוציה מרחבית ואנרגיה נמשכות. להתגבר על מכשולים אלו ידרוש חידוש מתמשך בציוד ובמתודולוגיות ניסיוניות, כפי שהודגש על ידי מוסדות מחקר מובילים כמו לורנס ברקלי לאומיות וחברת מקס פלאנק.

עוד הזדמנות משמעותית צפונה בחקר תופעות תלויות וקטור גלים בחומרים חדשים, כמו מבודדים טופולוגיים, חומרים דו-ממדיים ומטמטמטרים. מערכות אלו מציגות תכונות אלקטרוניות, אופטיות ואקוסטיות ייחודיות שבסיסן תלוי במבני הבנדים תלויות וקטור גלים שלהם. הבנת וניצול תכונות אלו יכולים להוביל לחדשות משמעותיות בקומפיוטר קוונטי, חילוץ אנרגיה ועיבוד מידע. ארגונים כמו המכון הלאומי לסטנדרטים וטכנולוגיה (NIST) פעילים לפתח תקנים וטכניקות מדידה לתמוך בחקר בתחומים אלו.

מודלים חישוביים וסימולציות גם מציבים כמויות ואתגרים. חיזוי מדויק של התנהגות תלוית וקטור גלים במערכות גדולות, מבולבלות או בתחומים קשורים לאחר הכביש דורש משאבים חישוביים משמעותיים ואלגוריתמים מתקדמים. חידושי חישוב בפיתוח ביצועים גבוהים, למידת מכונה, וגישות מונחות נתונים החלו להתגבר על אתגרים אלו, позволяя לחוקרים לחקור רגעי גזירת גלים שהם בלתי נגישים בעבר.

בהבנה בראיה קדימה, שיתוף פעולה בין תחומי נחוץ. ההתקדמות במחקר וקטור גלים תהיה תלויה בשילוב מומחיות מפיזיקה, מדעי חומרים, הנדסה ומדעי מחשב. ארגונים בינלאומיים כמו החברה האמריקאית לפיזיקה ואיגוד הבינלאומי לקריסטלוגרפיה משחקים תפקיד מרכזי בהנחלת שיתופי פעולה כאלו, ארגון כנסים והפצת פרקטיקות טובות.

לסיכום, בעוד שנותרו אתגרים טכניים ומושגיים משמעותיים, עתיד המחקר על וקטורי גלים משופע בהזדמנויות. השקעה מתמשכת בטכניקות ניסיוניות, כלים חישוביים ורשתות שיתוף פעולה יהיו המפתח לניהול את הפוטנציאל המלא של תופעות מונחות על ידי וקטור גלים במדע וטכנולוגיה.

מקורות וגורמי הפניה

Unlocking Quantum Power The Multiverse Explained!