Recent News

波ベクトルの力を解き放つ：量子と材料の洞察への鍵

Posted on
Unlocking the Power of Wavevector: The Key to Quantum and Material Insights

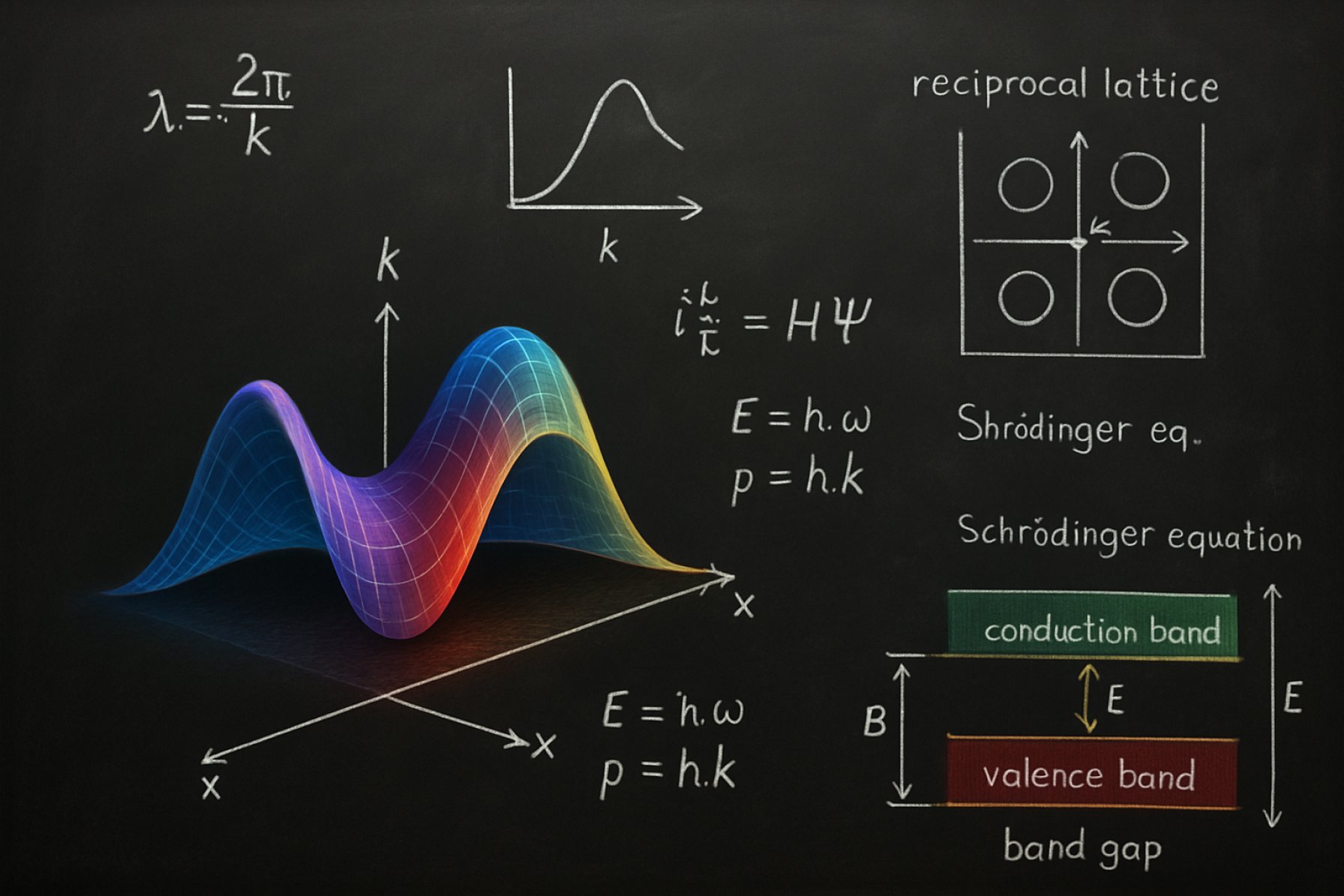
波ベクトルの解明：この基本的な概念が量子物理学、材料科学、およびそれを超えた分野にどのように影響を与えるか。波と粒子を支配する隠れたパターンを発見しましょう。

波ベクトルの紹介：定義と歴史的背景

波ベクトルの概念は、光学、音響、量子力学を含む物理学の波現象を研究する上で基本的なものです。波ベクトルは通常kという記号で表され、波の伝播方向と空間的周波数を特徴づけるベクトル量です。数学的には、波ベクトルの大きさは ( |k| = 2π/λ ) によって表され、ここで ( λ ) は波長です。波ベクトルの方向は、波が伝播する方向を指します。この二重の役割により、波ベクトルは電磁波、音波、粒子の量子力学的波動関数などの周期的現象を説明するための中心的なツールとなります。

歴史的には、波ベクトルの概念は、19世紀に波動理論が発展したことから生まれました。特に、科学者たちが光や音を波として数学的に表現しようと試みたことに伴い、波ベクトルの公式化が行われました。波ベクトルの公式化は、複雑な波形が傅里葉成分の和に分解されることを可能にする傅里葉分析の出現と密接に関連しています。結晶学および固体物理学の文脈において、波ベクトルは周期的格子内の電子およびフォノンの挙動を説明するために特に重要になりました。これはバンド理論とブリルアンゾーンの発展において顕著です。

現代物理学において、波ベクトルは不可欠です。たとえば、量子力学では、波ベクトルは粒子の運動量と直接関連しており、ド・ブロイ関係 ( p = ħk ) によって示されます。ここで ( ħ ) は縮小プランク定数です。この関係は量子理論の多くを支え、材料中の電子の挙動の研究において基盤となっています。光学においては、波ベクトルは異なる媒体における光の伝播を説明し、屈折や回折といった現象に影響を与えます。波ベクトルは波干渉の解析やフォトニックデバイスの設計にも重要な役割を果たします。

今日、波ベクトルは世界中の物理学および工学のカリキュラムで標準的な概念として教えられており、研究および産業で日常的に使用されています。アメリカ物理学会や物理学研究所などの組織が、現代の科学技術における波ベクトルの応用や意味に関する資源や刊行物を提供しています。

数学的基礎：ベクトルを使った波の表現

波ベクトルは、特に物理学や工学における波の数学的表現で基本的な概念です。波の方向と空間的周波数を記述するためのコンパクトで正確な方法を提供します。数学的には、波ベクトルはkという記号で表され、波の波長 (λ) に関連する大きさを持つベクトル量として定義され、関係式 |k| = 2π/λ で表されます。波ベクトルの方向は、波が伝播する方向を示します。

平面波の文脈において、波は位置と時間の関数として以下のように表現できます：

  • ψ(r, t) = A exp[i(k · r − ωt)]

ここで、ψは波動関数、Aは振幅、rは位置ベクトル、ωは角周波数、tは時間です。ドット積 k · r は、伝播方向に向かって波の位相が進むことを確実にします。この形式は、量子力学、光学、および音響学などの分野で波現象を分析するために広く使用されています。

波ベクトルは、波干渉、回折、異なる媒体における波の伝播の研究において重要な役割を果たします。たとえば、結晶学においては、逆格子の概念が波ベクトルに基づいて構築されており、X線回折パターンの解析や結晶構造の決定を可能にします。量子力学において、波ベクトルは粒子の運動量と直接関連しており、ド・ブロイ関係により示されます。p = ħk、ここでħは縮小プランク定数です。この関係は、現代物理学の中心にある波粒二重性の基礎を成しており、アメリカ物理学会などの組織によって説明されています。

さらに、波ベクトルの形式主義は、電気電子技術者協会 (IEEE) によって概説された電磁波の研究において不可欠です。これらの文脈において、波ベクトルはエネルギーの流れの方向を決定するだけでなく、屈折率などの物質的特性と相互作用して、屈折や反射のような現象に影響を与えます。

要約すると、波ベクトルは波を表現するための数学的に厳密で物理的に意味のある方法を提供し、波の空間的周期性と方向性を要約しています。その応用は複数の科学分野にまたがり、波動理論と分析の礎となっています。

量子力学における波ベクトル：運動量と不確実性

量子力学において、波ベクトルの概念は微視的スケールでの粒子の挙動を理解するために基本的です。波ベクトルは通常kとして表され、量子粒子に関連する波の空間的周波数を特徴づけるベクトル量です。波ベクトルは粒子の波動関数の波長 (λ) によって、関係式k = 2π/λで直接関連しています。波ベクトルの方向は波の伝播方向を示し、その大きさは波長に反比例します。

波ベクトルは、ド・ブロイ仮説によって説明される物質の波のような性質と粒子のような性質を結びつける重要な役割を果たします。この原理によれば、運動量pを持つ各粒子は、その波ベクトルがp = ħkで与えられる波に関連付けられます。ここでħは縮小プランク定数です。この関係は、平面波の観点から量子状態を数学的に表現する基礎を形成し、シュレーディンガー方程式を含む量子力学の形式主義の基盤を支えています。

波ベクトルは、ハイゼンベルクの不確実性原理の形成にも重要です。量子力学において、粒子の位置と運動量は同時に正確に決定することができず、その不確実性は逆に関連しています。運動量は波ベクトルに比例するため、波ベクトルの不確実性 (Δk) は運動量の不確実性 (Δp) に直接関連しています。そのため、不確実性原理はΔx · Δk ≥ 1/2のように表現でき、ここでΔxは位置の不確実性です。この関係は、粒子の位置とその関連する波ベクトルを同時に測定する際の内在的な制限を浮き彫りにしており、量子系の基本的な確率的性質を反映しています。

実践的には、波ベクトルは回折、干渉、固体の電子的特性などの現象を分析するために不可欠です。たとえば、固体物理学においては、波ベクトルは結晶格子内の電子の量子状態を表現するために使用され、エネルギーバンドとブリルアンゾーンの概念に繋がります。波ベクトルの正確な操作と測定は、電子顕微鏡や半導体デバイス工学のなどの技術において重要です。

波ベクトルの厳密な数学的扱いとその運動量および不確実性への影響は、アメリカ物理学会や物理学研究所といった組織によって確立される現代量子理論の基礎となっています。これらの組織は、量子力学における研究と教育の進展を促進し続けています。

結晶学および固体物理学における役割

結晶学および固体物理学において、波ベクトルの概念は、結晶などの周期的構造内の波（特に電子およびフォノン）の挙動を理解するために基本的です。波ベクトルは、通常kとして表され、媒体を通る波の方向および波長（あるいは同等に、運動量）を特徴づけるベクトル量です。その大きさは波長に反比例し、方向は波の伝播方向を示します。

結晶の文脈において、原子の周期的配置は逆格子の形成に繋がります。逆格子は、周期的システムにおける波現象の分析を簡素化する数学的構造です。波ベクトルはこの枠組みにおいて中心的な役割を果たし、Blochの定理を使用して電子状態や振動モード（フォノン）の記述を可能にします。Blochの定理に従えば、周期的ポテンシャル内の電子の波動関数は、格子の周期性を持つ関数によって調整された平面波として表現できます。このため、波ベクトルkはこれらの状態をラベル付けする量子数として機能し、その値は通常、逆空間でユニークに定義された領域である第1ブリルアンゾーンに制限されています。

波ベクトルの役割は、電子バンド構造の解析にも及び、これは材料の電気的、光学的、熱的特性を決定する上で重要です。電子のエネルギーと波ベクトルとの関係（E–k関係）は、結晶内の許可されたエネルギーバンドと禁止されたエネルギーバンドを明らかにし、材料が導体、半導体、絶縁体として機能するかを決定します。同様に、フォノン—量子化された格子振動—の分散関係は波ベクトルの関数として記述され、熱伝導率やその他の振動的性質についての洞察を提供します。

X線回折や中性子散乱といった実験技術は、結晶格子との衝突を解釈するために波ベクトルの概念に依存しています。これらの相互作用中の波ベクトルの変化は、結晶構造、原子位置、および材料内の動的プロセスに関する情報を提供します。国際結晶学連合（IUCR）やアメリカ物理学会などの組織は、これらの分野における研究の進展と方法論の標準化に重要な役割を果たしています。

要約すると、波ベクトルは結晶学と固体物理学の中で不可欠なツールであり、周期的固体における波現象の理論的記述と実験的調査の基盤を支えています。

波ベクトルと分散関係：波の伝播の理解

波ベクトルは波現象の研究において基本的な概念であり、波の方向と空間的周波数を特徴づけるベクトル量です。数学的には、波ベクトルは通常kとして定義され、波の位相の勾配であり、その大きさは波長に反比例します。三次元空間において、波ベクトルは波の位相が空間でどのように変化するかを簡潔に記述し、その方向は波の伝播方向を示し、その長さは ( |k| = 2π/λ ) で与えられます。ここで ( λ ) は波長です。

波ベクトルの重要性は、光学、音響、量子力学などのさまざまな物理学の分野に広がります。たとえば光学では、波ベクトルは光伝播、屈折、および回折の分析に中心的な役割を果たします。また、電磁波の研究においても重要であり、マクスウェル方程式によって記述されています。この文脈において、波ベクトルは光が異なる媒体でどのように振る舞うかを決定するのに役立ちます。光学およびフォトニクス分野の世界的な組織であるOptica（以前のアメリカ光学会）は、波現象の研究や応用のためのリソースや基準を提供しています。

固体物理学において、波ベクトルは結晶素材における電子やフォノンの挙動を記述する上で中心的な役割を果たします。たとえばブリルアンゾーンの概念は波ベクトルによって定義され、電子バンド構造を理解するために不可欠です。アメリカ物理学会は、凝縮物理システムにおける波ベクトルの研究と教育の進展を推進する権威ある組織です。

波ベクトルは量子力学における運動量の概念とも密接に関連しています。ド・ブロイ仮説によれば、粒子の運動量はその波ベクトルに直接比例し、( p = ħk )と表されます。ここで ( ħ ) は縮小プランク定数です。この関係は現代量子理論の多くを支え、波粒二重性の分析における基盤となっています。

全体として、波ベクトルは波の数学的記述に統一的なパラメータとして機能し、波の伝播、干渉、分散の分析を可能にします。その有用性は理論的枠組みと実用的応用の両方で明らかであり、現代物理学と工学の礎となっています。

光学およびフォトニクスにおける応用

波ベクトルの概念は、光学およびフォトニクスにおいて基本的であり、さまざまな媒体での光の伝播、相互作用、操作を理解するための礎となっています。波ベクトルは一般にkとして表され、波の伝播方向と空間的周波数（波長）を記述するベクトル量です。その大きさは波長に反比例し、方向はエネルギーの流れの方向を示します。光学およびフォトニクスにおいて、波ベクトルは屈折、回折、干渉、および複雑な材料内での光の挙動などの現象を分析するために重要です。

光学における波ベクトルの主な応用の1つは、異なる媒体を通る光の伝播の分析です。Optica（以前のOSA）によれば、異なる屈折率を持つ2つの材料の境界での波ベクトルの変化は、光の屈折を支配するスネルの法則の基礎となります。境界での波ベクトルの平行成分の保存は、光が表面でどのように屈折または反射するかを予測する上で不可欠であり、この原則はレンズ設計、ファイバー光学、フォトニックデバイス全般で広く使用されます。

フォトニクスにおいて、波ベクトルはフォトニック結晶やメタマテリアルの研究に中心的な役割を果たします。これらのエンジニアリング構造は屈折率の周期的な変化を作り出すことによって光の伝播を操作し、光が伝播できない周波数範囲を持つフォトニックバンドギャップを形成します。波ベクトルと周波数の関係はフォトニックバンド構造によって記述され、これにより材料内での光の許可されたモードと禁止されたモードが決まります。この原則は、高効率の導波路、光学フィルター、および自発的放出を制御するデバイスの開発に活用されています。これはマサチューセッツ工科大学 (MIT)の研究から際立っています。

波ベクトルの分析は、非線形光学の分野でも重要であり、相互作用する光子の波ベクトルの和が保存される必要がある位相整合条件は、第二高調波生成やパラメトリック増幅のような効率的な周波数変換プロセスを可能にします。これは、多くの現代のレーザーシステムや量子光源の動作を支えています。これはSPIE, 国際光学とフォトニクスの社会によって説明されています。

さらに、波ベクトルの形式主義は、光ファイバーの光パルスの分散と伝播を理解することがハイスピードデータ伝送にとって重要な光通信システムの設計および分析で不可欠です。波ベクトルの役割は、モード伝播と分散関係を記述することにより、全球通信ネットワークでの帯域幅と信号の完全性を最適化することを保証します。

計算シミュレーションとモデリングにおける波ベクトル

計算シミュレーションとモデリングにおいて、波ベクトルの概念は周期的現象を記述し分析する上で基本的です。特に、凝縮物理学、材料科学、および計算化学の分野において、波ベクトルは波の空間的周波数と方向を特徴付け、実空間と逆空間（運動量空間）における波の数学的表現の中心です。シミュレーションにおいて、波ベクトルは分子動力学、密度汎関数理論（DFT）、および格子動力学などの手法の結果を解釈するために重要です。

計算モデリングにおける波ベクトルの主な使用の1つは、周期的境界条件の分析です。物質の有限部分をシミュレーションする際、無限システムを模倣するために周期的境界条件が適用されることがよくあります。このようなシステムにおける許可された波ベクトルは、シミュレーションセルのサイズと形状によって量子化され、これらの離散的なkポイントは逆空間におけるブリルアンゾーンをサンプリングするために使用されます。このサンプリングは、電子バンド構造、フォノン分散関係、および光学スペクトルなどの特性を計算するために不可欠です。これらの計算の正確性は、サンプリングされた波ベクトルの密度と分布に依存しています。

電子構造計算、たとえばDFTを用いて行う計算において、波ベクトルは結晶固体における電子状態のラベル付けに使用されます。電子エネルギーバンドは波ベクトルの関数であり、その分散関係は材料の導電性、半導体性、または絶縁性を理解するための洞察を提供します。Quantum ESPRESSOやVASP（ウィーン第一原理シミュレーションパッケージ）などの計算パッケージは、効率的かつ正確な電子特性のモデリングを可能にする高度なアルゴリズムを実装しています。

同様に、格子動力学やフォノン計算において、波ベクトルは結晶中の原子の集団振動モードを記述します。フォノン分散関係は、波ベクトルの関数として振動周波数をプロットし、熱伝導率、比熱、およびその他の熱的性質を理解するために重要です。Phonopyなどのツールは、これらの目的のために広く使用されており、波ベクトル形式主義を駆使してフォノンスペクトルを計算し可視化します。

全体として、波ベクトルは実空間の原子配置と物理現象の逆空間表現を接続する架け橋として機能します。計算シミュレーションにおけるその役割は、原子および電子レベルでの材料特性を予測し解釈する上で不可欠であり、現代計算科学の中核的な概念となっています。

波ベクトルを測定するための実験技術

波ベクトルの測定は、特に凝縮物理学、光学、および材料科学の分野において実験物理学で基本的です。波ベクトルは一般にkとして示され、波の伝播の方向と大きさを特徴づけ、波長および周波数に直接関連しています。波ベクトルの正確な決定は、回折、干渉、および材料の電子構造などの現象を分析するために不可欠です。

波ベクトルを測定するために最も広く用いられる実験技術の1つはX線回折 (XRD)です。XRDでは、単色X線ビームが結晶サンプルに向けられ、回折ビームの角度と強度が測定されます。回折ピークの位置は特定の波ベクトルに対応し、ブラッグの法則を使用して決定されます。この技術は結晶構造を明らかにするために不可欠であり、国際結晶学連合などの組織によって標準化されています。

別の重要な方法は中性子散乱であり、これは特に材料内の磁気構造やダイナミクスを探るために貴重です。中性子ビームは、その中性の電荷と適切な波長のために原子核や磁気モーメントと相互作用し、散乱イベント中の波ベクトル転送を正確に測定することを可能にします。ラウエ＝ランゲビン研究所や標準技術研究所のような施設は、これらの実験のための高度な中性子源を運営しています。

表面科学の領域では、角度分解光電子分光法 (ARPES)は、固体の電子バンド構造を測定するための強力な技術です。材料を光子で照射し、放出された電子の運動エネルギーと放出角を分析することにより、研究者は結晶内での電子の初期波ベクトルを再構成できます。この方法は超伝導やトポロジカル絶縁体のような現象を研究するために重要であり、主要なシンクロトロン施設での研究によって支えられています。欧州シンクロトロン放射施設もその一つです。

光波においては、フーリエ変換分光法や干渉計法が一般的に用いられます。これらの技術は、光の空間的および時間的コヒーレンスを分析し、波ベクトル情報を抽出します。これはフォトニクスおよび光学工学で重要です。Optica（以前のOSA）は、これらの測定のためのリソースと基準を提供する組織です。

要約すると、波ベクトルを測定するための実験技術の選択は、波の種類（X線、中性子、電子、または光子）や、調査対象の材料またはシステムの特性に依存します。これらの方法の継続的な開発と洗練は、基礎科学と応用科学の両方の進展にとって中心的です。

新興技術における波ベクトル：ナノサイエンスとメタマテリアル

波ベクトルの概念は、新興技術の理解と発展において中心的です。特に、ナノサイエンスやメタマテリアルの分野において重要です。波ベクトルは一般にkとして表され、媒体内の波の伝播の方向と大きさを特徴づけます。ナノサイエンスでは、材料やデバイスが原子および分子スケールで工学されるため、波ベクトルは電子輸送、フォノンダイナミクス、光・物質相互作用などの現象を記述する上で重要です。たとえば、量子井戸、ワイヤー、量子ドットでは、空間的制約による波ベクトルの量子化が離散的エネルギーレベルを生じ、ナノ構造の電子および光学特性を根本的に変化させます。これは、ナノスケールトランジスタ、量子ドット、現代のナノテクノロジーの基盤となるその他のデバイスの動作の基盤となっています（ナンノテクノロジーイニシアチブ）。

メタマテリアル—自然界には存在しない特性を示すように設計された人工的構造—において、波ベクトルは電磁波がこれらの材料と相互作用する方法を決定する上で重要な役割を果たします。メタマテリアルは光の波ベクトルを操作できるように設計され、負の屈折、クローク、スーペルレンズなどの現象を可能にします。構成要素の周期性と幾何学をサブ波長スケールで調整することで、研究者は材料内での有効波ベクトルを制御し、新しい光学的および電磁的反応を生み出します。これは、高度なイメージングシステム、センサー、通信デバイスの開発に重要な意味を持っています（Optica（以前のアメリカ光学会））。

さらに、波ベクトル依存の現象の研究は、フォトニックおよびフォノニック結晶の設計において不可欠です。これらは、光子とフォノンの伝播に影響を与える周期的構造です。これらの結晶のバンド構造は、許可された波ベクトルと禁止された波ベクトルによって決定され、ナノスケールでの光や音の制御を可能にします。この能力は、効率的な発光ダイオードから新しい熱管理システムに至るまで、さまざまな応用に活用されています（IEEE）。

ナノサイエンスとメタマテリアルが進化し続ける中で、波ベクトルの正確な操作と理解は、研究と技術革新の最前線にあります。波ベクトル依存の特性を工学する能力は、情報処理、エネルギー収集、さらに進んだ材料とデバイスの次世代において新たなフロンティアを開いています。

今後の方向性：波ベクトル研究における課題と機会

波ベクトルの研究—波の伝播の方向と大きさを記述する量—は、物理学、材料科学、および工学の進展において中心的な役割を果たし続けています。研究が複雑なシステムに深く迫るにつれ、波ベクトル関連の調査の未来を形作るいくつかの課題と機会が見出されています。

主な課題の1つは、ますます複雑で小型化されるシステムにおける波ベクトルの正確な測定と操作にあります。たとえば、ナノフォトニクスや量子材料においては、原子またはサブ波長スケールで波ベクトルを解決し制御する能力が、次世代デバイスの開発にとって不可欠です。角度分解光電子分光法 (ARPES) や高度な電子顕微鏡などの技術がこれらのニーズに対応するために洗練されていますが、空間およびエネルギー解像度には依然として制限があります。これらの障壁を克服するためには、計測器と実験手法における継続的なイノベーションが必要です。これは、ローレンス・バークレー国立研究所やマックス・プランク協会などの主要な研究機関によって強調されています。

もう1つの重要な機会は、トポロジカル絶縁体、2D材料、メタマテリアルなどの新しい材料における波ベクトル依存の現象の探索です。これらのシステムは、波ベクトルに依存したバンド構造によって根本的に支配されるユニークな電子的、光学的、音響的特性を示します。これらの特性を理解し活用することは、量子コンピュータ、エネルギー収集、情報処理における画期的な進展をもたらす可能性があります。標準技術研究所 (NIST)のような組織は、この研究の最前線をサポートするための標準や測定技術を積極的に開発しています。

計算モデリングとシミュレーションもまた、課題と機会を提供します。大きく、無秩序な、または強く相関したシステムにおける波ベクトル依存の挙動を正確に予測するには、膨大な計算リソースと高度なアルゴリズムが必要です。高性能コンピューティング、機械学習、およびデータ駆動型アプローチの進展が、これらの課題に取り組み始めており、研究者が波ベクトル空間の以前はアクセスできなかった領域を探索できるようになります。

今後の展望として、学際的コラボレーションが不可欠です。波ベクトルの研究の進展は、物理学、材料科学、工学、コンピュータ科学の専門知識の統合によって支えられます。アメリカ物理学会や国際結晶学連合のような国際組織は、そのようなコラボレーションを促進し、会議を開催し、ベストプラクティスを普及させる上で重要な役割を果たしています。

要約すると、技術的および概念的な課題は依然として多く残っていますが、波ベクトル研究の未来は豊かな機会で満ちています。実験技術、計算ツール、および協力ネットワークへの継続的な投資が、科学と技術における波ベクトル駆動現象の潜在能力を引き出すための鍵となるでしょう。

出典と参考文献

Unlocking Quantum Power The Multiverse Explained!

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です