Golfvector Gedemystificeerd: Hoe Dit Fundamentele Concept Kwantumfysica, Materiaalkunde en Meer Vormgeeft. Ontdek de Verborgen Patronen Die Golven en Deeltjes Beheersen.

• Inleiding tot Golfvector: Definitie en Historische Context
• Wiskundige Fundamenten: Het Representeren van Golven met Vectoren
• Golfvector in Kwantummechanica: Momentum en Onzekerheid
• Rol in Kristallografie en Vastestoffysica
• Golfvector en Dispersieverhoudingen: Begrijpen van Golfverspreiding
• Toepassingen in Optica en Fotonica
• Golfvector in Rekenkundige Simulaties en Modellering
• Experimentele Technieken voor het Meten van Golfvectors
• Golfvector in Opkomende Technologieën: Nanowetenschap en Metamaterialen
• Toekomstige Richtingen: Uitdagingen en Kansen in Golfvector Onderzoek
• Bronnen & Referenties

Inleiding tot Golfvector: Definitie en Historische Context

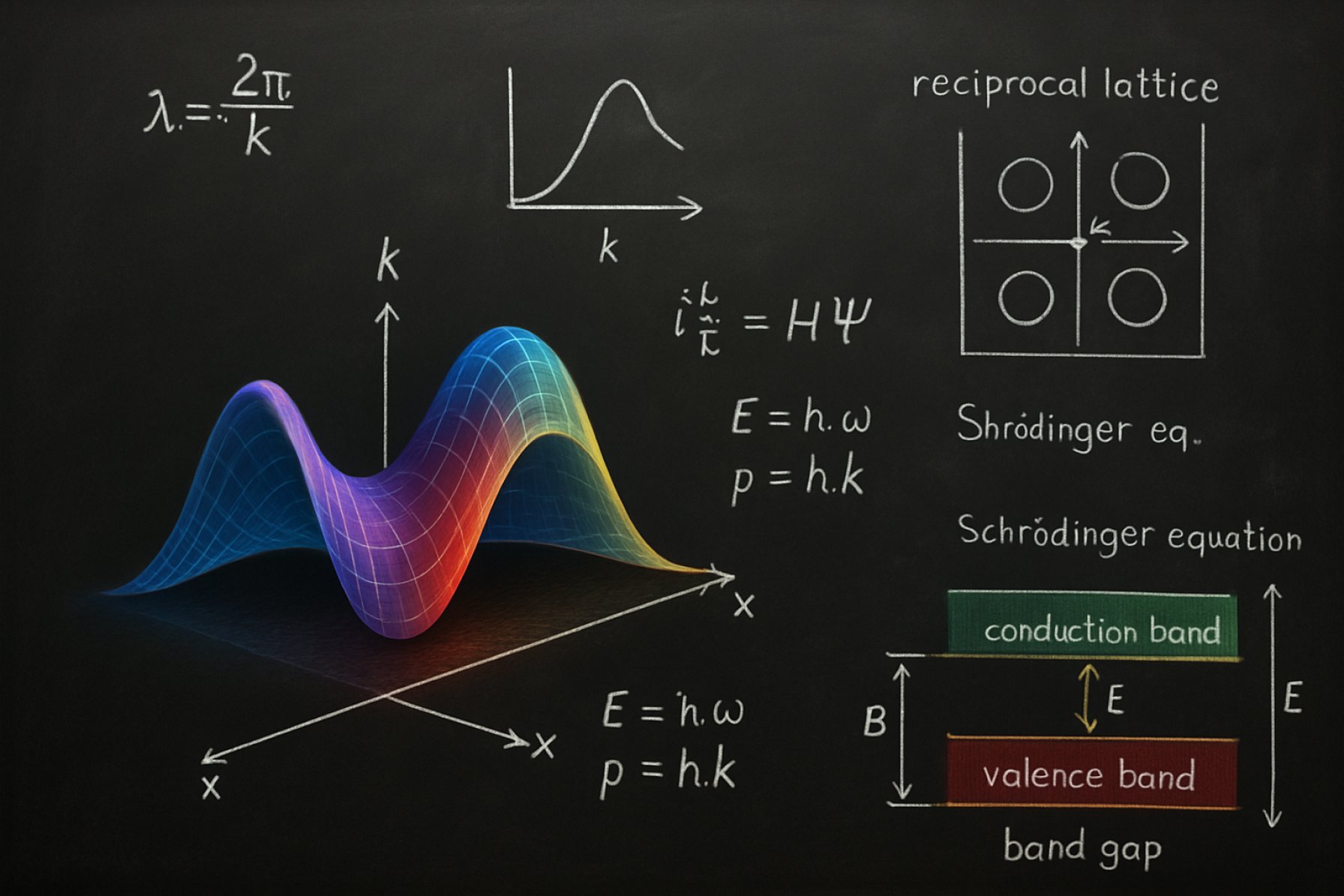
Het concept van de golfvector is fundamenteel in de studie van golfverschijnselen binnen de natuurkunde, inclusief optica, akoestiek en kwantummechanica. Een golfvector, meestal aangeduid met het symbool k, is een vectoriële grootheid die zowel de propagatierichting als de ruimtelijke frequentie van een golf karakteriseert. Wiskundig is de grootte van de golfvector gegeven door ( |k| = 2pi/lambda ), waarbij ( lambda ) de golflengte is. De richting van de golfvector wijst in de richting waarin de golf zich voortplant. Deze duale rol maakt de golfvector een centraal hulpmiddel in het beschrijven van periodieke fenomenen, zoals elektromagnetische golven, geluidsgolven en de kwantummechanische golffuncties van deeltjes.

Historisch gezien is het concept van de golfvector voortgevloeid uit de ontwikkeling van de golftheorie in de 19e eeuw, vooral toen wetenschappers probeerden licht en geluid wiskundig als golven te beschrijven. De formalisering van de golfvector was nauw verbonden met de opkomst van Fourier-analyse, die het mogelijk maakte complexe golfvormen te decomponeren in sommen van sinusvormige componenten, elk gekarakteriseerd door een specifieke golfvector. In de context van kristallografie en vastestoffysica werd de golfvector vooral belangrijk voor het beschrijven van het gedrag van elektronen en fononen in periodieke netwerken, zoals zichtbaar wordt in de ontwikkeling van bandtheorie en Brillouin-zones.

In de moderne natuurkunde is de golfvector onmisbaar. In de kwantummechanica, bijvoorbeeld, is de golfvector rechtstreeks gerelateerd aan het momentum van een deeltje via de de Broglie-relatie ( p = hbar k ), waarbij ( hbar ) de gereduceerde Planck-constante is. Deze relatie vormt de basis van veel van de kwantumtheorie en is fundamenteel in de studie van het elektronische gedrag in materialen. In de optica beschrijft de golfvector de voortplanting van licht in verschillende media, wat invloed heeft op fenomenen zoals breking en diffractie. De golfvector speelt ook een cruciale rol in de analyse van golfinterferentie en het ontwerp van fotonische apparaten.

Tegenwoordig is de golfvector een standaardconcept dat wereldwijd in natuurkunde- en ingenieurscurricula wordt onderwezen en dat routinematig wordt gebruikt in onderzoek en de industrie. Organisaties zoals de American Physical Society en het Institute of Physics bieden middelen en publicaties die de toepassingen en implicaties van de golfvector in de hedendaagse wetenschap en technologie verder verkennen.

Wiskundige Fundamenten: Het Representeren van Golven met Vectoren

De golfvector is een fundamenteel concept in de wiskundige representatie van golven, vooral in natuurkunde en engineering. Het biedt een compacte en nauwkeurige manier om zowel de richting als de ruimtelijke frequentie van een golf te beschrijven. Wiskundig wordt de golfvector aangeduid met het symbool k en wordt gedefinieerd als een vectoriële grootheid waarvan de grootte gerelateerd is aan de golflengte (λ) van de golf via de relatie |k| = 2π/λ. De richting van de golfvector geeft de richting aan waarin de golf zich voortplant.

In de context van een vlakke golf kan de golf worden weergegeven als een functie van positie en tijd met de uitdrukking:

• ψ(r, t) = A exp[i(k · r − ωt)]

waarbij ψ de golffunctie is, A de amplitude is, r de positievector is, ω de hoeksfrequentie is en t de tijd is. Het inwendige product k · r zorgt ervoor dat de fase van de golf in de richting van voortplanting vordert. Deze formalism is wijdverbreid in vakgebieden zoals kwantummechanica, optica en akoestiek om golfverschijnselen te analyseren.

De golfvector speelt een cruciale rol in de studie van golfinterferentie, diffractie en de voortplanting van golven in verschillende media. Bijvoorbeeld, in de kristallografie is het concept van de reciprocale rooster gebaseerd op de golfvector, waardoor de analyse van röntgendiffractiepatronen en de bepaling van kristalstructuren mogelijk is. In de kwantummechanica is de golfvector rechtstreeks gerelateerd aan het momentum van een deeltje via de de Broglie-relatie, p = ħk, waarbij ħ de gereduceerde Planck-constante is. Deze relatie vormt de basis voor de golf-deeltje dualiteit die centraal staat in de moderne natuurkunde, zoals beschreven door organisaties zoals de American Physical Society.

Bovendien is de golfvectorformalisme essentieel in de studie van elektromagnetische golven, zoals uiteengezet door het Institute of Electrical and Electronics Engineers (IEEE). In deze contexten bepaalt de golfvector niet alleen de richting van de energiestroom, maar interageert ook met materiaaleigenschappen, zoals de brekingsindex, om fenomenen zoals breking en reflectie te beïnvloeden.

Samenvattend biedt de golfvector een wiskundig rigoureuze en fysiek significante manier om golven te representeren, waarbij zowel hun ruimtelijke periodiciteit als richting wordt omvat. De toepassingen beslaan meerdere wetenschappelijke disciplines, waardoor het een hoeksteen is van de golftheorie en analyse.

Golfvector in Kwantummechanica: Momentum en Onzekerheid

In de kwantummechanica is het concept van de golfvector fundamenteel voor het begrijpen van het gedrag van deeltjes op microscopische schalen. De golfvector, doorgaans aangeduid als k, is een vectoriële grootheid die de ruimtelijke frequentie van een golf die verband houdt met een kwantumdeeltje karakteriseert. Het is rechtstreeks gerelateerd aan de golflengte (λ) van de golffunctie van het deeltje via de relatie k = 2π/λ. De richting van de golfvector geeft de richting van golfvoortplanting aan, terwijl zijn grootte omgekeerd evenredig is met de golflengte.

De golfvector speelt een cruciale rol in het verbinden van de golfachtige en deeltjeachtige eigenschappen van materie, zoals beschreven door de de Broglie-hypothese. Volgens dit principe kan elk deeltje met momentum p worden geassocieerd met een golf waarvan de golfvector is gegeven door p = ħk, waarbij ħ de gereduceerde Planck-constante is. Deze relatie vormt de basis voor de wiskundige beschrijving van kwantumtoestanden in termen van vlakke golven en vormt de basis voor de formalisme van de kwantummechanica, inclusief de Schrödinger-vergelijking.

De golfvector is ook centraal in de formulering van het onzekerheidsprincipe van Heisenberg. In de kwantummechanica kunnen de positie en het momentum van een deeltje niet beide nauwkeurig worden bepaald; hun onzekerheden zijn omgekeerd gerelateerd. Aangezien het momentum evenredig is met de golfvector, is de onzekerheid in de golfvector (Δk) direct verbonden met de onzekerheid in momentum (Δp). Het onzekerheidsprincipe kan dus worden uitgedrukt als Δx · Δk ≥ 1/2, waarbij Δx de onzekerheid in positie is. Deze relatie benadrukt de intrinsieke beperkingen bij het gelijktijdig meten van de positie van een deeltje en de bijbehorende golfvector, wat de fundamentele probabilistische aard van kwantumsystemen weerspiegelt.

In praktische termen is de golfvector essentieel voor het analyseren van verschijnselen zoals diffractie, interferentie en de elektronische eigenschappen van vaste stoffen. Bijvoorbeeld, in de vastestoffysica wordt de golfvector gebruikt om de kwantumtoestanden van elektronen in een kristallat te beschrijven, wat leidt tot het concept van energiebanden en de Brillouin-zone. De precieze manipulatie en meting van golfvectors zijn cruciaal in technologieën zoals elektronenmicroscopie en de engineering van halfgeleiderapparaten.

De rigoureuze wiskundige behandeling van golfvectors en hun implicaties voor momentum en onzekerheid is fundamenteel voor de moderne kwantumtheorie, zoals vastgesteld door pionierswerk van organisaties zoals de American Physical Society en het Institute of Physics, die blijven bijdragen aan onderzoek en onderwijs in de kwantummechanica.

Rol in Kristallografie en Vastestoffysica

In de kristallografie en vastestoffysica is het concept van de golfvector fundamenteel om het gedrag van golven—bijzonder elektronen en fononen—binnen periodieke structuren zoals kristallen te begrijpen. De golfvector, vaak aangeduid als k, is een vectoriële grootheid die zowel de richting als de golflengte (of equivalente momentum) van een golf die zich door een medium voortplant, karakteriseert. De grootte is omgekeerd evenredig met de golflengte, en de richting geeft de richting van voortplanting aan.

In de context van kristallen leidt de periodieke ordening van atomen tot de vorming van een reciprocale rooster, een wiskundig construct dat de analyse van golffenomenen in periodieke systemen vereenvoudigt. De golfvector is centraal in dit kader, omdat het mogelijk maakt om elektronentoestanden en vibratiemodi (fononen) te beschrijven met behulp van de stelling van Bloch. Volgens de stelling van Bloch kunnen de golffuncties van elektronen in een periodiek potentieel worden uitgedrukt als een vlakke golf gemoduleerd door een functie met de periodiciteit van het rooster. De golfvector k fungeert dus als een kwantumgetal dat deze toestanden labelt, en de waarden zijn typisch beperkt tot de eerste Brillouin-zone, een uniek gedefinieerde regio in de reciprocale ruimte.

De rol van de golfvector strekt zich uit tot de analyse van elektronische bandstructuren, die cruciaal zijn voor het bepalen van de elektrische, optische en thermische eigenschappen van materialen. De relatie tussen de energie van een elektron en zijn golfvector (de E–k-relatie) onthult de toegestane en verboden energiebanden in een kristal, wat bepaalt of een materiaal zich gedraagt als een geleider, halfgeleider of isolator. Evenzo worden de dispersieverhoudingen voor fononen—gequantiseerde roostertrillingen—beschreven als functies van de golfvector, wat inzicht geeft in thermische geleidbaarheid en andere vibrerende eigenschappen.

Experimentele technieken zoals röntgendiffractie en neutronenscattering zijn gebaseerd op het concept van de golfvector om de interactie van incidentele golven met het kristalrooster te interpreteren. De verandering in golfvector tijdens deze interacties geeft informatie over de kristalstructuur, atoomposities en dynamische processen binnen het materiaal. Organisaties zoals de International Union of Crystallography en de American Physical Society spelen een sleutelrol bij het bevorderen van onderzoek en het standaardiseren van methodologieën in deze velden.

Samenvattend is de golfvector een onmisbaar hulpmiddel in de kristallografie en vastestoffysica, dat de theoretische beschrijving en experimentele onderzoek van golffenomenen in periodieke vaste stoffen ondersteunt.

Golfvector en Dispersieverhoudingen: Begrijpen van Golfverspreiding

De golfvector is een fundamenteel concept in de studie van golfverschijnselen, als een vectoriële grootheid die zowel de richting als de ruimtelijke frequentie van een golf karakteriseert. Wiskundig is de golfvector, vaak aangeduid als k, gedefinieerd als de gradiënt van de fase van de golf, en de grootte is omgekeerd evenredig met de golflengte. In driedimensionale ruimte biedt de golfvector een beknopte beschrijving van hoe de fase van een golf varieert in de ruimte, waarbij de richting de richting van de golfvoortplanting aangeeft en de lengte wordt gegeven door ( |k| = 2pi/lambda ), waarbij ( lambda ) de golflengte is.

Het belang van de golfvector strekt zich uit over verschillende takken van de natuurkunde, inclusief optica, akoestiek en kwantummechanica. In de optica, bijvoorbeeld, is de golfvector centraal in de analyse van lichtvoortplanting, breking en diffractie. Het is ook cruciaal in de studie van elektromagnetische golven, zoals beschreven door de Maxwell-vergelijkingen, waar de golfvector helpt om het gedrag van licht in verschillende media te bepalen. Optica (voorheen Optical Society of America) is een toonaangevende organisatie op het gebied van optica en fotonica die middelen en standaarden biedt voor de studie en toepassing van golfverschijnselen.

In de vastestoffysica speelt de golfvector een belangrijke rol bij het beschrijven van het gedrag van elektronen en fononen in kristallijne materialen. Het concept van de Brillouin-zone is bijvoorbeeld gedefinieerd in termen van de golfvector en is essentieel voor het begrijpen van elektronische bandstructuren. De American Physical Society is een prominente autoriteit in het bevorderen van onderzoek en onderwijs in de natuurkunde, inclusief de studie van golfvectors in gecondenseerde stofsystemen.

De golfvector is ook nauw verbonden met het concept van momentum in de kwantummechanica. Volgens de de Broglie-hypothese is het momentum van een deeltje rechtstreeks evenredig met zijn golfvector, ( p = hbar k ), waarbij ( hbar ) de gereduceerde Planck-constante is. Deze relatie vormt de basis voor veel van de moderne kwantumtheorie en is fundamenteel in de analyse van golf-deeltje dualiteit.

Over het algemeen dient de golfvector als een verenigende parameter in de wiskundige beschrijving van golven, waarmee de analyse van golfvoortplanting, interferentie en dispersie in een breed scala van fysische systemen mogelijk wordt. Het nut is duidelijk in zowel theoretische kaders als praktische toepassingen, waardoor het een hoeksteen is van de moderne natuurkunde en techniek.

Toepassingen in Optica en Fotonica

Het concept van de golfvector is fundamenteel in optica en fotonica, als een hoeksteen voor het begrijpen van de voortplanting, interactie en manipulatie van licht in verschillende media. De golfvector, doorgaans aangeduid als k, is een vectoriële grootheid die zowel de voortplantingsrichting als de ruimtelijke frequentie (golflengte) van een golf beschrijft. De grootte is omgekeerd evenredig met de golflengte, en de richting geeft de richting van energiestroom aan. In optica en fotonica is de golfvector cruciaal voor het analyseren van fenomenen zoals breking, diffractie, interferentie en het gedrag van licht in complexe materialen.

Een van de primaire toepassingen van de golfvector in de optica is de analyse van lichtvoortplanting door verschillende media. Volgens Optica (voorheen OSA) is de verandering in de golfvector op de interface tussen twee materialen met verschillende brekingsindices de basis van Snell’s Law, dat de breking van licht regelt. De behoud van de parallelle component van de golfvector bij grenzen is essentieel voor het voorspellen van hoe licht buigt of reflecteert op oppervlakten, een principe dat veelvuldig wordt gebruikt in lensontwerp, vezeloptica en fotonische apparaten.

In fotonica is de golfvector centraal in de studie van fotonische kristallen en metamaterialen. Deze geengineerde structuren manipuleren de voortplanting van licht door periodieke variaties in de brekingsindex te creëren, wat leidt tot de vorming van fotonische bandgaten—frequentiebereiken waar licht niet kan voortplanten. De relatie tussen de golfvector en frequentie, beschreven door de fotonische bandstructuur, bepaalt de toegestane en verboden modi van licht binnen deze materialen. Dit principe wordt benut bij de ontwikkeling van uiterst efficiënte golflijnen, optische filters en apparaten voor het controleren van spontane emissie, zoals benadrukt door onderzoek van organisaties zoals het Massachusetts Institute of Technology (MIT).

Golfvectoranalyse is ook vitaal in het gebied van niet-lineaire optica, waar de fase-matchingvoorwaarde—die vereist dat de som van de golfvectors van interagerende fotonen behouden blijft—efficiënte frequentieconversieprocessen zoals tweede-harmonische generatie en parametrische versterking mogelijk maakt. Dit vormt de basis voor de werking van veel moderne lasersystemen en kwantumlichtbronnen, zoals beschreven door SPIE, de internationale vereniging voor optica en fotonica.

Bovendien is de golfvectorformalisme onmisbaar in het ontwerp en de analyse van optische communicatiesystemen, waarbij het begrijpen van de dispersie en voortplanting van lichtpulsen in optische vezels cruciaal is voor hoge datatransmissiesnelheden. De rol van de golfvector in het beschrijven van modale voortplanting en dispersieverhoudingen verzekert de optimalisering van bandbreedte en signaalintegriteit in wereldwijde telecommunicatienetwerken.

Golfvector in Rekenkundige Simulaties en Modellering

In rekenkundige simulaties en modellering is het concept van de golfvector fundamenteel voor het beschrijven en analyseren van periodieke fenomenen, vooral in velden zoals gecondenseerde stoffysica, materiaalkunde en computationele chemie. De golfvector, doorgaans aangeduid als k, karakteriseert de ruimtelijke frequentie en richting van een golf, en is centraal in de wiskundige representatie van golven in zowel reële als reciprocale (momentum) ruimte. In simulaties is de golfvector cruciaal voor het interpreteren van de resultaten van technieken zoals moleculaire dynamica, dichtheidsfunctionaaltheorie (DFT) en roosterdynamica.

Een van de primaire toepassingen van de golfvector in computationele modellering is de analyse van periodieke grensvoorwaarden. Bij het simuleren van een eindig deel van een materiaal worden vaak periodieke grensvoorwaarden toegepast om een oneindig systeem na te bootsen. De toegestane golfvectors in zo’n systeem zijn gequantiseerd volgens de grootte en vorm van de simulatiecel, en deze discrete k-punten worden gebruikt om de Brillouin-zone in de reciprocale ruimte te bemonsteren. Deze bemonstering is essentieel voor het berekenen van eigenschappen zoals elektronische bandstructuren, fonon-dispersieverhoudingen en optische spectra. De nauwkeurigheid van deze berekeningen hangt af van de dichtheid en distributie van de bemonsterde golfvectors.

In elektronische structuurcalculaties, zoals die uitgevoerd worden met behulp van DFT, wordt de golfvector gebruikt om de elektronentoestanden in kristallijne vastestoffen te labelen. De elektronische energiebanden zijn functies van de golfvector, en hun dispersieverhoudingen bieden inzicht in de geleidende, halfgeleidende of isolerende natuur van materialen. Computationele pakketten zoals Quantum ESPRESSO en VASP (Vienna Ab initio Simulation Package) implementeren geavanceerde algoritmes voor k-punt bemonstering, waardoor efficiënte en nauwkeurige modellering van elektronische eigenschappen mogelijk is.

Evenzo, in roosterdynamica en fononcalculaties, beschrijft de golfvector de collectieve trillingsmodi van atomen in een kristal. De fonon-dispersieverhoudingen, die trillingsfrequenties als functie van de golfvector plotten, zijn cruciaal voor het begrijpen van thermische geleidbaarheid, specifieke warmte en andere thermodynamische eigenschappen. Hulpmiddelen zoals Phonopy worden veel gebruikt voor deze doeleinden en maken gebruik van de golfvectorformalisme om fononspectra te berekenen en te visualiseren.

Over het algemeen fungeert de golfvector als een brug tussen reële ruimtelijke configuraties van atomen en reciprocale ruimtelijke representaties van fysische fenomenen. De rol in rekenkundige simulaties is onmisbaar voor het voorspellen en interpreteren van de eigenschappen van materialen op atomair en elektronisch niveau, waardoor het een hoeksteenconcept is in de moderne computationele wetenschap.

Experimentele Technieken voor het Meten van Golfvectors

De meting van golfvectors is fundamenteel in de experimentele natuurkunde, vooral in velden zoals gecondenseerde stoffysica, optica en materiaalkunde. De golfvector, doorgaans aangeduid als k, karakteriseert de richting en grootte van de voortplanting van een golf en is rechtstreeks gerelateerd aan zijn golflengte en frequentie. Nauwkeurige bepaling van golfvectors maakt de analyse van fenomenen zoals diffractie, interferentie en de elektronische structuur van materialen mogelijk.

Een van de meest gebruikte experimentele technieken voor het meten van golfvectors is röntgendiffractie (XRD). In XRD wordt een monochromatische röntgenbundel gericht op een kristallijn monster, en de hoeken en intensiteiten van de gediffractieerde bundels worden gemeten. De posities van de diffractiepieken komen overeen met specifieke golfvectors, die worden bepaald met behulp van de wet van Bragg. Deze techniek is essentieel voor het verduidelijken van kristalstructuren en is gestandaardiseerd door organisaties zoals de International Union of Crystallography.

Een andere belangrijke methode is neutronenscattering, die bijzonder waardevol is voor het onderzoeken van magnetische structuren en dynamica in materialen. Neutronbundels, vanwege hun neutrale lading en geschikte golflengte, interageren met atomische kernen en magnetische momenten, waardoor een precieze meting van de golfvectorverandering tijdens de scattered gebeurtenissen mogelijk is. Faciliteiten zoals het Institut Laue-Langevin en het National Institute of Standards and Technology exploiteren geavanceerde neutronbronnen voor dergelijke experimenten.

In het domein van de oppervlaktewetenschap is hoek-resolved photo-emissiespectroscopie (ARPES) een krachtige techniek voor het meten van de elektronische bandstructuur van vaste stoffen. Door een materiaal te bestralen met fotonen en de kinetische energie en emisshoeken van de geëjecteerde elektronen te analyseren, kunnen onderzoekers de initiële golfvectors van de elektronen binnen het kristal reconstrueren. Deze methode is cruciaal voor het bestuderen van fenomenen zoals supergeleiding en topologische isolatoren en wordt ondersteund door onderzoek bij belangrijke synchrotronfaciliteiten, waaronder de European Synchrotron Radiation Facility.

Voor optische golven worden Fourier-transform spectroscopie en interferometrie vaak gebruikt. Deze technieken analyseren de ruimtelijke en temporele coherentie van licht om informatie over de golfvector te extraheren, wat van vitaal belang is in fotonica en optische techniek. Organisaties zoals het Optica (voorheen OSA) bieden middelen en standaarden voor deze metingen.

Samenvattend hangt de keuze van de experimentele techniek voor het meten van golfvectors af van het type golf (röntgen-, neutron-, elektron-, of foton) en de specifieke eigenschappen van het materiaal of systeem dat onderzocht wordt. De voortdurende ontwikkeling en verfijning van deze methoden zijn centraal voor vooruitgang in zowel fundamentele als toegepaste wetenschap.

Golfvector in Opkomende Technologieën: Nanowetenschap en Metamaterialen

Het concept van de golfvector is centraal in het begrijpen en bevorderen van opkomende technologieën, vooral in de velden van nanowetenschap en metamaterialen. De golfvector, doorgaans aangeduid als k, karakteriseert de richting en grootte van de golfvoortplanting in een medium. In de nanowetenschap, waar materialen en apparaten worden gecreëerd op atomair en moleculair niveau, is de golfvector cruciaal voor het beschrijven van fenomenen zoals elektronentransport, fonon-dynamica en licht-materie interacties. Bijvoorbeeld, in kwantumputten, draden en stippen leidt de kwantisering van de golfvector door ruimtelijke opsluiting tot discrete energieniveaus, waardoor de elektronische en optische eigenschappen van nanostructuren fundamenteel veranderen. Dit ondersteunt de werking van nanoschaaltransistoren, kwantumstippen en andere apparaten die de ruggengraat van de moderne nanotechnologie vormen (National Nanotechnology Initiative).

In het domein van metamaterialen—kunstmatig gestructureerde materialen die zijn ontwikkeld om eigenschappen te vertonen die niet in de natuur worden gevonden—speelt de golfvector een cruciale rol in het bepalen hoe elektromagnetische golven met deze materialen interageren. Metamaterialen zijn ontworpen om de golfvector van licht te manipuleren, waardoor fenomenen zoals negatieve breking, cloaking en superlensvorming mogelijk worden. Door de periodiciteit en geometrie van de samenstellende elementen op subgolflengte schalen te optimaliseren, kunnen onderzoekers de effectieve golfvector binnen het materiaal beheersen, wat leidt tot nieuwe optische en elektromagnetische reacties. Dit heeft aanzienlijke implicaties voor de ontwikkeling van geavanceerde imaging systemen, sensoren en communicatietoestellen (Optica (voorheen Optical Society of America)).

Bovendien is de studie van golfvector-afhankelijke fenomenen essentieel voor het ontwerp van fotonische en fononische kristallen, die periodieke structuren zijn die de voortplanting van fotonen en fononen respectievelijk beïnvloeden. De bandstructuur van deze kristallen, bepaald door de toegestane en verboden golfvectors, maakt het mogelijk licht en geluid op nanoschaal te beheersen. Deze mogelijkheid wordt benut voor toepassingen variërend van efficiënte lichtgevende diodes tot nieuwe thermomanagementsystemen (IEEE).

Naarmate nanowetenschap en metamaterialen blijven evolueren, blijft de precieze manipulatie en het begrip van de golfvector aan de voorhoede van onderzoek en technologische innovatie. De mogelijkheid om golfvector-afhankelijke eigenschappen te creëren opent nieuwe grenzen in informatieverwerking, energieopslag en meer, wat de fundamentele rol van dit concept in de volgende generatie geavanceerde materialen en apparaten benadrukt.

Toekomstige Richtingen: Uitdagingen en Kansen in Golfvector Onderzoek

De studie van golfvectors—grootheden die zowel de richting als de grootte van de golfvoortplanting beschrijven—blijft centraal in de vooruitgang van natuurkunde, materiaalkunde en engineering. Terwijl het onderzoek dieper ingaat op complexe systemen, ontstaan er verschillende uitdagingen en kansen die de toekomst van golfvector-gerelateerde onderzoeken zullen vormgeven.

Een van de belangrijkste uitdagingen ligt in de nauwkeurige meting en manipulatie van golfvectors in steeds complexere en miniaturiseerde systemen. In nanophotonics en kwantummaterialen, bijvoorbeeld, is de mogelijkheid om golfvectors op atomair of subgolflengte schaal te resolven en te controleren cruciaal voor de ontwikkeling van apparaten van de volgende generatie. Technieken zoals hoek-resolved photo-emissiespectroscopie (ARPES) en geavanceerde elektronenmicroscopie worden verfijnd om aan deze behoeften te voldoen, maar beperkingen in ruimtelijke en energie-resolutie blijven bestaan. Het overwinnen van deze barrières vereist voortdurende innovatie in instrumentatie en experimentele methoden, zoals benadrukt door toonaangevende onderzoeksinstellingen zoals het Lawrence Berkeley National Laboratory en de Max Planck Society.

Een andere aanzienlijke kans is de verkenning van golfvector-afhankelijke fenomenen in nieuwe materialen, zoals topologische isolatoren, 2D-materialen en metamaterialen. Deze systemen vertonen unieke elektronische, optische en akoestische eigenschappen die fundamenteel worden bepaald door hun golfvector-afhankelijke bandstructuren. Het begrijpen en benutten van deze eigenschappen zou kunnen leiden tot doorbraken in kwantumcomputing, energieopslag en informatieverwerking. Organisaties zoals het National Institute of Standards and Technology (NIST) ontwikkelen actief standaarden en meettechnieken om deze onderzoeksgrens te ondersteunen.

Computational modellering en simulatie bieden ook zowel uitdagingen als kansen. Het nauwkeurig voorspellen van golfvector-afhankelijke gedragingen in grote, ontslagen of sterk gecorreleerde systemen vereist aanzienlijke computermiddelen en geavanceerde algoritmes. Vooruitgang in high-performance computing, machine learning en data-gedreven benaderingen beginnen deze uitdagingen aan te pakken, waardoor onderzoekers eerder ontoegankelijke regimes van golfvectorruimte kunnen verkennen.

Met het oog op de toekomst zal interdisciplinaire samenwerking essentieel zijn. Vooruitgang in golfvectoronderzoek zal afhangen van de integratie van expertise uit de natuurkunde, materiaalkunde, techniek en computerwetenschap. Internationale organisaties zoals de American Physical Society en de International Union of Crystallography spelen een cruciale rol in het bevorderen van dergelijke samenwerkingen, het organiseren van conferenties en het verspreiden van best practices.

Samenvattend, terwijl er aanzienlijke technische en conceptuele uitdagingen blijven bestaan, is de toekomst van golfvectoronderzoek rijk aan kansen. Voortdurende investeringen in experimentele technieken, computationele hulpmiddelen en samenwerkingsnetwerken zullen cruciaal zijn voor het ontsluiten van het volledige potentieel van golfvector-gedreven fenomenen in wetenschap en technologie.

Bronnen & Referenties

• Institute of Electrical and Electronics Engineers (IEEE)
• International Union of Crystallography
• Massachusetts Institute of Technology (MIT)
• SPIE, de internationale vereniging voor optica en fotonica
• Quantum ESPRESSO
• VASP
• Institut Laue-Langevin
• National Institute of Standards and Technology
• European Synchrotron Radiation Facility
• Optica
• National Nanotechnology Initiative
• Lawrence Berkeley National Laboratory
• Max Planck Society